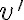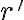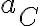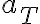una idea de como hacer el ejercicio?
y mira yo encaje los versores en direccion radial y tangencial como siempre, y t planteas q la posicion es r = x.er donde "x" es una funcion q dice la distancia al centro d giro, despues planteas fuerzas y eso.
la aceleracion segun er me quedo x'' - x(omega)2 donde omega es la velocidad angular q t dan ahi
la aceleracion segun er me quedo x'' - x(omega)2 donde omega es la velocidad angular q t dan ahi
Hola
¿como llegaste a ese resultado?
Yo no puedo llegar a nada coherente, que utilizaste como
y 
en las ecuaciones de 
y 
, etc?
¿como llegaste a ese resultado?
Yo no puedo llegar a nada coherente, que utilizaste como
y en las ecuaciones de y , etc?
mira yo pongo un versor er radial y un ephi en la direccion tangencial y de ahi tengo q: r=xer
v=x'er +xwephi
a= (x''-xw2)er +2x'wephi
despues d fuerzas puse una normal segun ephi, el peso y una normal opuesta al peso digamos.
para la parte A) tenes que segun er x''-w2x=0
resolviendo esa ecuacion t queda que x(t)=(vo/2w)*(ewt-e-wt)
que es lo mismo que (vo/w)*senh(wt)
parte B) en la ecuacion segun ephi tenes que m2x'w=Normal intengrando la x(t)
de la parte A y haciendo cuentas a cara d topo llegas a que
N=m(g2 + (2wvocosh(wt))2)(1/2)
v=x'er +xwephi
a= (x''-xw2)er +2x'wephi
despues d fuerzas puse una normal segun ephi, el peso y una normal opuesta al peso digamos.
para la parte A) tenes que segun er x''-w2x=0
resolviendo esa ecuacion t queda que x(t)=(vo/2w)*(ewt-e-wt)
que es lo mismo que (vo/w)*senh(wt)
parte B) en la ecuacion segun ephi tenes que m2x'w=Normal intengrando la x(t)
de la parte A y haciendo cuentas a cara d topo llegas a que
N=m(g2 + (2wvocosh(wt))2)(1/2)
como puedo encarar la parte (C). Yo despeje el tiempo de r(t)=L+R/2 pero me quda medio intratable para despejar la velocidad.
y mira yo hice esto.... d la parte "a" tenes la ecuacion del movimiento radial, entonces eso lo metes en la ecuacion de la velocidad que es:
v=x'(er)+x.(omega).(etita)
entonces te queda que v=v0.cosh(omega.t)+v0.senh(omega.t) lo del coseno segun el versor radial y el seno segun el tangencial
despues sabes que en el tiempo final la componente tangencial de la velocidad es "L.omega"
despues tenes que 1=cosh2-senh2 con eso cambias lo que estaba en coseno y haces lo mismo de que el seno va a valer "L.omega" y ahi t da que v=L.omega(tangencial)+(v02+L2.omega2)(1/2)(radial)
capaz salia mas rapido x otro camino pero no c me ocurrio, esto se entendio?
v=x'(er)+x.(omega).(etita)
entonces te queda que v=v0.cosh(omega.t)+v0.senh(omega.t) lo del coseno segun el versor radial y el seno segun el tangencial
despues sabes que en el tiempo final la componente tangencial de la velocidad es "L.omega"
despues tenes que 1=cosh2-senh2 con eso cambias lo que estaba en coseno y haces lo mismo de que el seno va a valer "L.omega" y ahi t da que v=L.omega(tangencial)+(v02+L2.omega2)(1/2)(radial)
capaz salia mas rapido x otro camino pero no c me ocurrio, esto se entendio?
Hola, me parece que para la parte B del Ej 15 si tienes en cuenta que solo te sirve la parte de la aceleración según (phi) y tienes que es m2x'w=Normal como vos ya tienes x(t) si derivas en vez de integrar y sabiendo que N= m2x'w(phi) – mg(k) te queda N=2mwvcosh(wt) según e(phi)-mg según( k) que es la solución , espero les sirva. saludos