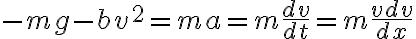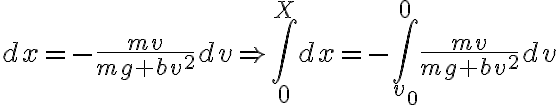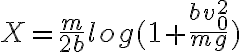, nos vemos en la facu gente linda
estuve pensando las formas de integrar, probé con pre integración como dimos en el teórico pero no llego a nada, si alguien sabe las 2 formas de integrar para hallar las respuestas y me tira alguna línea, se agradece , nos vemos en la facu gente linda
, nos vemos en la facu gente linda
hola mira vs sabes que: F=m(dv/dt)
entonces despejando... dt=mdv/F
despues integras y allas el tiempo integras entre 0 y velocidad final
la parte 2 no se como sacarla
la fuerza depende de la velocidad asi q no la podes sacar de la integral como una constante espero te sirva
entonces despejando... dt=mdv/F
despues integras y allas el tiempo integras entre 0 y velocidad final
la parte 2 no se como sacarla
la fuerza depende de la velocidad asi q no la podes sacar de la integral como una constante espero te sirva
gracias michael, re sirvió el tip pero tengo un problema con el signo que no lo entiendo porque yo tengo -bv^2+mg=mdv/dt con el versor j definido hacia arriba según mi sistema de referencia, entonces así no me da arctg como en las soluciones, si coloco un sg+ al primer término si llego a la solución de arctg pero igual me da la misma solución pero con un sg-, se entiende? no sé como interpretar el sg inicial creo, si alguien se da cuenta, explique gracias!
YO TENGO LA MISMA ECUACION QUE VOS Y LLEGUE AL RESULTADO, NADA MAS QUE EL SIGNO DEL PESO ES CON UN -, SI TENES ALGUNA DUDA TE EXPLICO PASO A PASO LO QUE HICE,
LA SEGUNDA PARTE A ALGUIEN LE SALIO? PORQUE YO PARTI DE LA MISMA ECUACION NADA MAS QUE LE HICE UN CAMBIO DE VARIABLE A V^2 = U(X) Y TA DE AHI ME QUEDA QUE a=du/dt y me queda una ecuacion lineal de primer orden du/dt(u punto) + 2b/mu=-2g
y la resuelvo y al final despejo a v(t) que es la raiz de la solucion (u(x)) a esa velocidad la igualo a 0 porque se que cuando sea la altura maxima la velocidad es cero y trato de despejar hmax y me queda como la solucion nada mas que lo de adentro del logaritmo neperiano me queda como (mg/bvo^2)
alguien que me ayude
Un poco tarde pero logré hacer la parte a2. Escribo la deducción por si a alguien le sirve:
Aplicando newton considerando positivo hacia arriba, tenemos:
Hice uso de las definiciones de velocidad y aceleración; lo que logro jugando así con los diferenciles es hacer aparecer el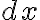 
que me lleva a lo que queiro. Despejando 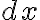de lo anterior e integrando:
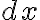que me lleva a lo que queiro. Despejando 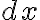de lo anterior e integrando:En esa ultima ecuacion, el primer miembro es 
, la altura que se pide, y el segundo es una integral que sale fácil haciendo el cambio de variable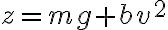 
. Me dio:
, la altura que se pide, y el segundo es una integral que sale fácil haciendo el cambio de variable 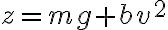. Me dio:Espero que sirva, saludos!
yo me tome el eje de referencia hacia abajo y me olvide de las matematicas
si te fijas la fuerza peso, la viscoza y la aceleracion apuntan en el mismo sentido asi q me tome TODO positivo o sea: mg+bv=mdv/dt
supongo por ahi tiene q salir sino mañana antes de 11:30 estoy en la biblio arriva no me jode si queres preguntarme
si te fijas la fuerza peso, la viscoza y la aceleracion apuntan en el mismo sentido asi q me tome TODO positivo o sea: mg+bv=mdv/dt
supongo por ahi tiene q salir sino mañana antes de 11:30 estoy en la biblio arriva no me jode si queres preguntarme