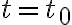 es:
es: 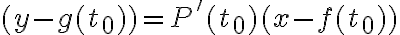 , con
, con 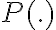 ecuacion implícita de la curva.
ecuacion implícita de la curva.Mi duda es si está bien agragar eso en la hipotésis, el tema es que no me acuerdo de donde sale esa fórmula, la di en el liceo...
 es la recta que pasa por el punto
es la recta que pasa por el punto 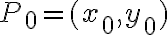 con la direcciòn del vector
con la direcciòn del vector 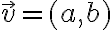 , la misma en forma paramètrica se escribe:
, la misma en forma paramètrica se escribe: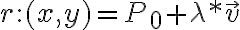 una ecuaciòn vectorial que equivale a las dos ecuaciones escalares
una ecuaciòn vectorial que equivale a las dos ecuaciones escalares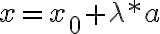

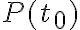 y que es tangente a la curva; esto ùltimo lo obtenemos agarrando como vector director a cualquier vector tangente. El mismo vector tangente
y que es tangente a la curva; esto ùltimo lo obtenemos agarrando como vector director a cualquier vector tangente. El mismo vector tangente 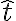 es una opciòn vàlida, pero tambièn sirve (y en este caso es màs conveniente) usar simplemente el vector
es una opciòn vàlida, pero tambièn sirve (y en este caso es màs conveniente) usar simplemente el vector 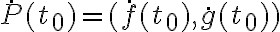 . Teniendo en cuenta esto y lo que dije antes, obtenes la expresiòn que te piden demostrar.
. Teniendo en cuenta esto y lo que dije antes, obtenes la expresiòn que te piden demostrar.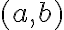 es siempre perpendicular a
es siempre perpendicular a 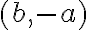 con lo cual el vector
con lo cual el vector 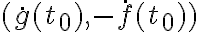 siempre es normal a la curva. Ese te sirve.
siempre es normal a la curva. Ese te sirve.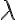 . En ese caso lo que debes hacer es redefinirte convenientemente el paràmetro como el que ya tenes por algùn mùltiplo de las componentes del vector tangente que elegiste.
. En ese caso lo que debes hacer es redefinirte convenientemente el paràmetro como el que ya tenes por algùn mùltiplo de las componentes del vector tangente que elegiste.