Hola en la solucion. al momento de ser Karnaugh a d0, el resultado es d0=e0'tpi' + e1tpi' + tpfd'i' + e0tpfd', y para mi es d0=e0'tpi' + e1tpi', no entiendo porque hace el recuadro en rojo ni el que esta en azul.
En respuesta a Luciano Jesus Montero Videla
Re: Examen febrero 2013 - Karnaugh
Agrego esta imagen, entiendo porque se hace tanto el cuadrado negro como el amarillo, no entiendo porque se hace el azul ni el rojo, no estan demas?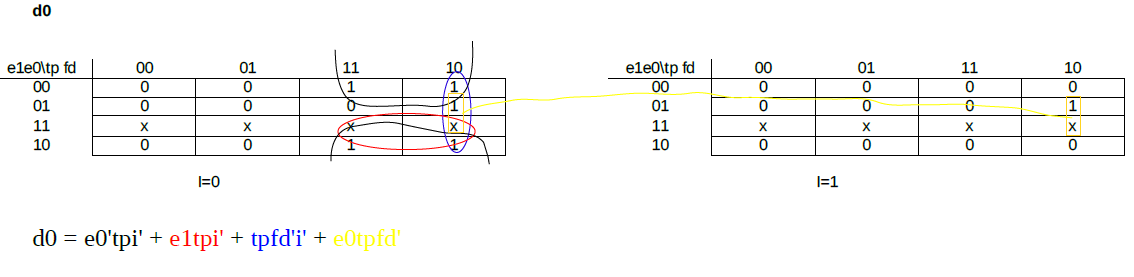
En respuesta a Luciano Jesus Montero Videla
Re: Examen febrero 2013 - Karnaugh
A mi me queda d0=e0´tp i´+ e0 tp fd´ . Osea el negro y el amarillo. No probe todos los casos, pero creo que los 2 dan el mismo resultado... fijate , por ejemplo el azul, te viene como entrada tpdf´i´ , si e0=1 pasa por el amarillo, si e0=0 pasa por el negro. Y un razonamiento similar pasa con el rojo. No se si se entendio....
No creo que este mal, solo que fue armando los cuadrados con un orden distinto (rojo, negro, azul y amarillo en ese orden, te queda igual a la solucion y cumplis con lo que te dice karnaugh).
Si esta mal que me corrijan.
Saludos!
Hola!
Esa solución es incorrecta! Deberían estar englobados únicamente el negro y el amarillo como bien dijeron. Estuve mirando la solución y hay otros diagramas sobreenglobados. No se fíen mucho y cualquier cosa pregunten :)
Saludos!
Alguien podria explicar porque el azul estaria mal?... no lo veo..
Osea la idea del karnaugh es intentar hacer los cuadros mas grandes posibles tal que la cantidad de elementos dentro del cuadro sea una potencia de 2, y los cuadros se terminan cuando ya no queda ningun 1 que no pertenezca a algun cuadro...
Por lo tanto si primero se hace el cuadro negro, despues queda un 1 sin cuadro asignado ( para e1.e0.tp.fd.i = 01100 ) entonces se busca un cuadro para ese 1 y el cuadro mas grande posible es la columna entera. Despues se compara los 2 karnaugh ( el de i = 0 y i = 1), y se ve que el bloque de i=1 esta incluido en un bloque del i = 0, entonces a mi me quedo lo siguiente:
d0 = e0'tp.i' + tp.fd'.i' + e0.tp.fd'
En respuesta a Gonzalo Alvaro Arcos Silva
Re: Examen febrero 2013 - Karnaugh
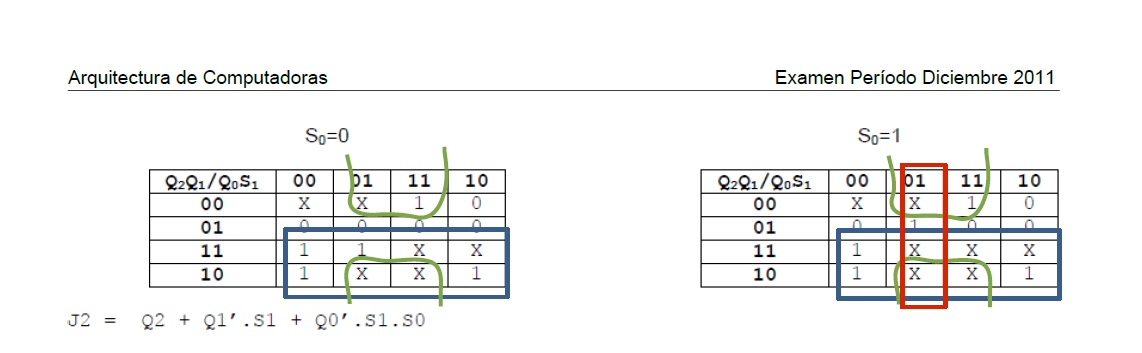
Esto sacado del examen diciembre 2011, no me queda claro porque, si es que esta mal el azul en el examen de febrero 2013, aca esta bien el rojo, no deberia ser el rojo un cuadro con solo un elemento, el elemento del casillero 0101 ?(asumiendo que el cuadro azul de 02/2013 esta mal, y siguiendo la misma logica entonces)..
Por eso pregunto cual de las 2 formas es..
En respuesta a Gonzalo Alvaro Arcos Silva
Re: Examen febrero 2013 - Karnaugh
Para mi ese caso de diciembre 2011 esta bien, y lo que esta mal del de febrero 2013 es el rojo, según los 1's y x's que allí aparecen(no realice todo el procedimiento, solo "interpreto" esos valores)
Saludos
En respuesta a Gerardo Fabian Coscia De Leon
Re: Examen febrero 2013 - Karnaugh
de Federico Rivero -
Estimados:
La idea de los mapas de Karnaugh es agrupar los unos en un conjunto mínimo de conjuntos, para minimizar la expresión. Una buena manera de verificar que su diagrama esté bien es verificar que ningún grupo se pueda agrandar sin agrupar ceros (de este modo, el grupo podría ser más grande sin cambiar el resultado lógico de la función), y que ningún grupo se pueda eliminar y que queden todos los 1's envueltos.
En los mapas del examen de febrero 2013, el grupo azul y el rojo se podrían eliminar, y los 1's seguirían todos agrupados por los grupos negro y amarillo. Esto NO puede hacerse con el grupo rojo del examen de diciembre 2011. Pues si lo quitan queda un 1 sin agrupar.
Un consejo más: encontrar el conjunto de grupos más grande posible mínimo que los encierre a todos NO significa que deban comenzar por el más grande! Eso en general lleva a soluciones incorrectas.
Cualquier duda pregunten!
Saludos,
Federico
ok, solo para confirmar ultima pregunta.. en el examen 2011 el cuadro rojo bordo tambien esta de mas no?
En respuesta a Gonzalo Alvaro Arcos Silva
Re: Examen febrero 2013 - Karnaugh
Para mi el bordo esta demas y falta un cuadro de 4 que incluya el 1 que no esta marcado, o sea que incluya 0000,0001,1000,1001 siendo el formato q2q1q0s1, es asi?
Es correcto :)
Saludos!
En respuesta a Federico Rivero
Re: Examen febrero 2013 - Karnaugh
Entendidio, gracias. Entonces puede ser que el siguiente al siguiente Karnaugh, el de luces, también este incorrecto? a mi me quedo lo siguiente:
luces= !e1 e0 !tp + e0 fd + !e0 tp i
Saludos, gracias
En respuesta a Gerardo Fabian Coscia De Leon
Re: Examen febrero 2013 - Karnaugh
Perdón, no tenia actulizada la conversación cuando respondí, mi pregunta se sigue refiriendo al de feb2013.
Comparto el resultado de Luciano
Saludos
En respuesta a Federico Rivero
Re: Examen febrero 2013 - Karnaugh
que tal Federico:
después de leer tus recomendaciones para la construcción de mapa de k. no entiendo en el ejercicio de feb2013 porque estaría mal la elipse azul, ya que como tu decís, si agrando el amarillo hasta el azul, no encierro ceros, en I=0.
Saludos gracias
En respuesta a Gerardo Fabian Coscia De Leon
Re: Examen febrero 2013 - Karnaugh
de Federico Rivero -
No se si entendí bien lo que dijiste, pero no podés agrandar sólo el rectángulo amarillo del diagrama izquierdo, pues te quedaría un globo de 6.
Si entendí mal por favor aclarame, pero ese globito azul es incorrecto :D
Saludos!
Federico
Volviendo al examen 2013, la expresión en rojo de d1 es e1tp, tp no debe estar negado?. Para mi es e1tp'
No entiendo. Gracias.
En respuesta a Federico Rivero
Re: Examen febrero 2013 - Karnaugh
Entendiste bien. Debo tener un error conceptual.
Para resolver estos ejercicios (k. de 5 variables) lo que hago es primero agrupo unos en el diagrama de la 5 variable negativa(el de la izquierda) como un k de 4 típico y después lo mismo con el de la derecha, pero agrupo de forma independiente, luego veo donde coniciden y donde no para calcular la expresion final. Creo que el error viene por el lado de la agrupación de unos de forma independiente entre ambos diagramas, puede ser?
Saludos, gracias
En respuesta a Gerardo Fabian Coscia De Leon
Re: Examen febrero 2013 - Karnaugh
de Federico Rivero -
Si, ese es el problema. Es como si en el diagrama de 4 resolvieras el rectángulo superior de 2x4 primero y luego el inferior de 2x4. No llegarías al óptimo.
Saludos,
Federico
En respuesta a Federico Rivero
Re: Examen febrero 2013 - Karnaugh
Gracias, me quedó bastante mas claro
Saludos