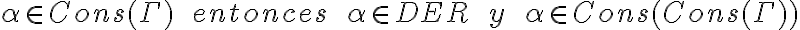Parciales

Hola,

Para probar la igualdad de conjuntos, usas que están mutuamente incluídos. Esto es: 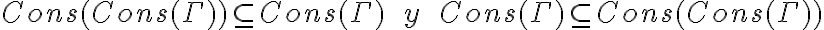$Cons(Cons(\Gamma))\subseteq Cons(\Gamma) \;\; y \;\; Cons(\Gamma)\subseteq Cons(Cons(\Gamma))$
Para probar la primera inclusión:

Te tomas 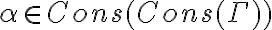$\alpha \in Cons(Cons(\Gamma))$ entonces existe una derivación 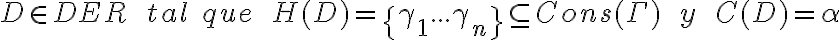$D \in DER \;\; tal \; que \;\; H(D)=\left \{\gamma_{1}...\gamma_{n} \right \}\subseteq Cons(\Gamma) \;\; y \;\; C(D)=\alpha$. A su vez existen 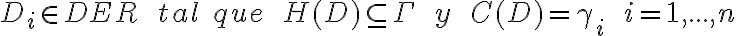$D_{i} \in DER \;\; tal \; que \;\; H(D)\subseteq\Gamma \;\; y \;\; C(D)=\gamma_{i} \;\; i=1,...,n$ entonces 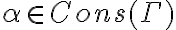$\alpha \in Cons(\Gamma)$  y tenes probada la primera inclusión.

La segunda inclusión:

Sea $\alpha \in Cons(\Gamma) \;\; entonces \;\; \alpha \in DER \;\; y \;\; \alpha \in Cons(Cons(\Gamma))$.

Como se cumplen las dos inclusiones son el mismo grupo.

Esa demostración tengo yo, espero se entienda algo. Saludos!