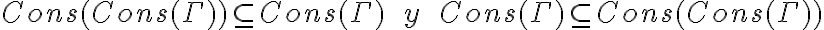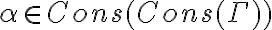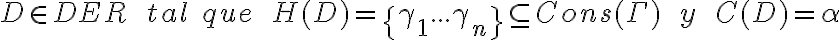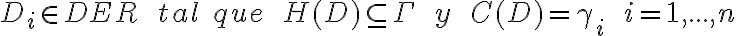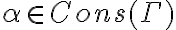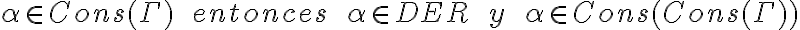Bueno, estoy mirando practicos para tener bien las propiedades que rondan conceptos de consistente maximal, etc., y viendo una respuesta de una pregunta, lei que alguien dijo que CONS(Gamma) = CONS(CONS(Gamma)) se probaba en un ejercicio de practico?
Estoy intentando demostrarlo yo pero ya no puedo pensar mas si esta bien o no, alguien sabe si efectivamente esta en un practico? Porque no lo encuentro.
Algo asi quizas la demostracion:
Para todo Fi perteneciente a CONS(gamma), Gamma deriva a Fi por def.
<--> (completitud)
Gamma Union Fi Deriva a Fi
<---> (consistencia)
CONS(gamma) Deriva a Fi
<---> (def cons)
Fi pertenece a CONS(CONS(Gamma))