Sea L un lenguaje de primer orden con igualdad de tipo de similaridad <-; 2; 1>
Considere ademas la estructura M = < N; +; 1>.
a. Defina inductivamente el conjunto TERM de los terminos y el conjunto FORM de las formulas correspondientes al lenguaje L.
b. Defina una funcion swap : TERM -> TERM que intercambia los argumentos de cada símbolo de funcion f. Por ejemplo: swap(f(c; f(x; y))) = f(f(y; x); c).
c. Demuestre inductivamente que para todo t que pertenece TERMC; M |= t = swap(t), donde TERMC es el conjunto de los terminos cerrados.
d. Indique si la siguiente oracion es verdadera o falsa, justificando adecuadamente.
para todo φ que pertenece a FORM, para todo t que pertenece a TERMC;M |= φ[t/x] <-> φ[swap(t)/x]
No sé cómo resolver la parte d..
Si me pueden ayudar..
Muchas gracias..
Verónica
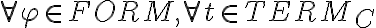
![\displaystyle {\mathrm M}\vDash \left( \varphi \left[ {}^{t}\!\!\diagup\!\!{}_{x}\; \right]\leftrightarrow \varphi \left[ {}^{\text{swap}\left( t \right)}\!\!\diagup\!\!{}_{x}\; \right] \right)](https://eva.fing.edu.uy/filter/tex/pix.php/9d59ef9f6532dd0635ce10c9dc9822bb.png "\displaystyle {\mathrm M}\vDash \left( \varphi \left[ {}^{t}\!\!\diagup\!\!{}_{x}\; \right]\leftrightarrow \varphi \left[ {}^{\text{swap}\left( t \right)}\!\!\diagup\!\!{}_{x}\; \right] \right)")
![\displaystyle \left( 2.4.5 \right)\Leftrightarrow \forall \varphi \in FORM,\forall t\in TER{{M}_{C}}\text{ }\left( {\mathrm M}\vDash \varphi \left[ {}^{t}\!\!\diagup\!\!{}_{x}\; \right]\text{ sii }\varphi \left[ {}^{\text{swap}\left( t \right)}\!\!\diagup\!\!{}_{x}\; \right] \right)](https://eva.fing.edu.uy/filter/tex/pix.php/61513d21de6654571eda90b2a8c5c2a2.png "\displaystyle \left( 2.4.5 \right)\Leftrightarrow \forall \varphi \in FORM,\forall t\in TER{{M}_{C}}\text{ }\left( {\mathrm M}\vDash \varphi \left[ {}^{t}\!\!\diagup\!\!{}_{x}\; \right]\text{ sii }\varphi \left[ {}^{\text{swap}\left( t \right)}\!\!\diagup\!\!{}_{x}\; \right] \right)")
![\displaystyle \left( \text{teorema de sustitucion y parte anterior} \right)\Leftrightarrow \forall \varphi \in FORM,\forall t\in TER{{M}_{C}}\text{ }\left( {\mathrm M}\vDash \varphi \left[ {}^{t}\!\!\diagup\!\!{}_{x}\; \right]\text{ sii }{\mathrm M}\vDash \varphi \left[ {}^{t}\!\!\diagup\!\!{}_{x}\; \right] \right) \displaystyle \checkmark](https://eva.fing.edu.uy/filter/tex/pix.php/e8ae977351192c87636ce1640c4838ab.png "\displaystyle \left( \text{teorema de sustitucion y parte anterior} \right)\Leftrightarrow \forall \varphi \in FORM,\forall t\in TER{{M}_{C}}\text{ }\left( {\mathrm M}\vDash \varphi \left[ {}^{t}\!\!\diagup\!\!{}_{x}\; \right]\text{ sii }{\mathrm M}\vDash \varphi \left[ {}^{t}\!\!\diagup\!\!{}_{x}\; \right] \right) \displaystyle \checkmark")