Foro para preguntas de Relaciones

Hola, me gustaría saber si lo que hice es correcto, además si los fundamentos son válidos. La letra dice lo siguiente:

(I) La relación es reflexiva? Esto significa que 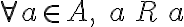$\forall a \in A, \; a \, R \, a$ . Podemos encontrar un ejemplo a partir de la negación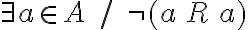 $\exists a \in A \; / \; \neg (a \, R \, a)$

Por ejemplo (1,1), entonces no es reflexiva.

(II) la definición de simetría dice que 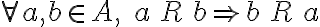$\forall a, b \in A, \; a \, R \, b \Rightarrow b \, R \, a$ . En este caso 1R2, pero 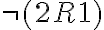$\neg(2R1)$ Por lo tanto no es simétrica. 

(III) es asimétrica? Debe cumplir que 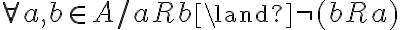$\forall a,b \in A / aRb \land \neg (bRa)$ donde a puede ser igual a b. Sin embargo 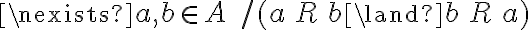$\nexists a, b \in A \;/ (a \, R \, b \land b \, R \, a)$   Entonces es asimétrica. 

(IV) para saber si es antisimétrica, basta con ir a la definición: 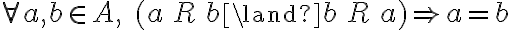$\forall a, b \in A, \; (a \, R \, b \land b \, R \, a) \Rightarrow a = b$ . Como 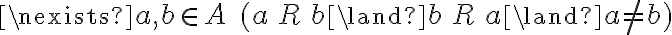$\nexists a, b \in A \; (a \, R \, b \land b \, R \, a \land a \ne b)$ entonces es antisimétrica. 

(V) la definición de transitividad dice lo siguiente: 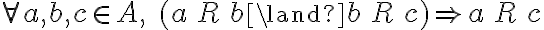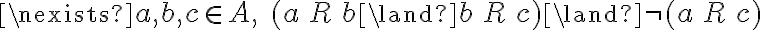$\forall a, b, c \in A, \; (a \, R \, b \land b \, R \, c) \Rightarrow a \, R \, c$ ,  $\nexists a, b, c \in A, \; (a \, R \, b \land b \, R \, c) \land \neg (a \, R \, c)$ (esto último se cumple), por lo tanto es transitiva.