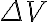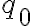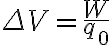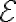Estimado,
lo que planteás para el calculo del trabajo en el caso de campos eléctricos conservativos es correcto. En los casos que el campo eléctrico es generado por cargas eléctricas se genera un campo de fuerza conservativo. Esto permite definir el trabajo como la variación de energía potencial y a partir de esta definir un potencial eléctrico 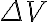 .
.
Esto ocurre porque tenemos fuentes y sumideros de campo eléctrico (las cargas).
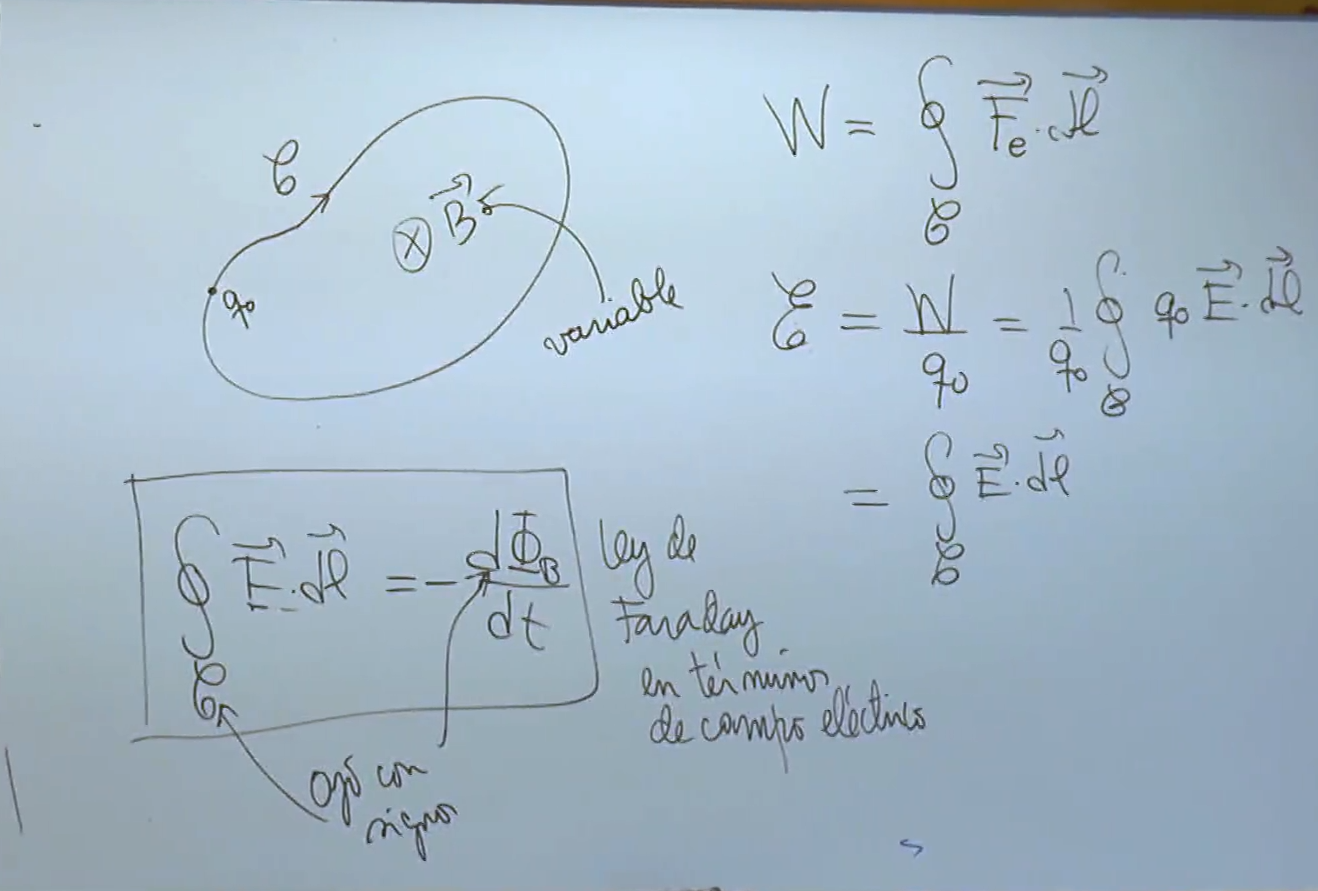
En el caso en que el campo eléctrico es inducido por una variación de flujo magnético, se generan lineas de campo eléctrico cerradas (sin fuentes o sumideros) similares a las de campo magnético que inducen las corrientes.
Este campo eléctrico no genera un campo conservativo, por lo que no puede usarse el concepto de energía potencial. En este caso, si integramos este campo multiplicado por una carga de prueba 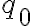 en un camino cerrado obtenemos un cierto trabajo (pues integramos una fuerza). Esto demuestra que no es un campo conservativo en este caso pero además nos permite definir el
en un camino cerrado obtenemos un cierto trabajo (pues integramos una fuerza). Esto demuestra que no es un campo conservativo en este caso pero además nos permite definir el 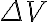 en este caso en que no hay un potencial asociado. Esto se hace de la forma
en este caso en que no hay un potencial asociado. Esto se hace de la forma
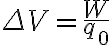
Es la única forma de definirlo pues no tenemos una energía potencial en este caso. Este 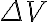 cuando fue descubierto se le dio el nombre de Fuerza Electro Motriz (F.E.M.) o
cuando fue descubierto se le dio el nombre de Fuerza Electro Motriz (F.E.M.) o 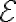 y por eso seguimos usando ese nombre.
y por eso seguimos usando ese nombre.
Saludos, Enzo.
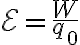 (o de manera análoga el trabajo sobre la carga de prueba es
(o de manera análoga el trabajo sobre la carga de prueba es 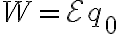 ) . Pensé que ese trabajo salía de la igualdad
) . Pensé que ese trabajo salía de la igualdad 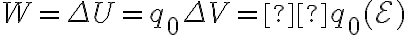 pero supuestamente esa igualdad es cuando el campo eléctrico es CONSERVATIVO, cosa que acá no sucede.
pero supuestamente esa igualdad es cuando el campo eléctrico es CONSERVATIVO, cosa que acá no sucede.