Estimado,
Es cierto que el libro enuncia la ley de Gauss sin dar una demostración rigurosa.
Una explicación conceptual es que la integral de campo eléctrico a través de una superficie cerrada es igual a todas las lineas de campo eléctrico que la atraviesan. Estas lineas solo cambian de cantidad si algo las genera o absorbe, de ahí que se puede hacer un vinculo directo entre las lineas que atraviesan una superficie y las cargas que las originan.
Una explicación más rigurosa surge del teorema de la divergencia de Gauss, el cual dice que la integral en una superficie cerrada de una función vectorial (el campo eléctrico) es igual a la integral en el volumen (que esta superficie encierra) de la divergencia de dicha función vectorial. La divergencia de un campo vectorial son los puntos donde se originan los campos (en este caso las cargas). Es decir que la integral de la carga contenida en el volumen es igual al flujo de campo que atraviesa la superficie.
Esta explicación se deja para el curso de electromagnetismo pues requiere conceptos de cálculo vectorial y estos no son previas de Física 3.
Saludos, Enzo
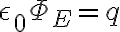, o es lo mismo que 
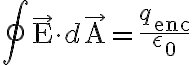donde la integral cerrada representaría el flujo del campo eléctrico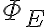 
?
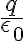