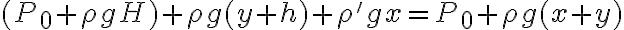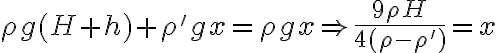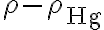Buenas! No estoy logrando dar con la solución del ejercicio
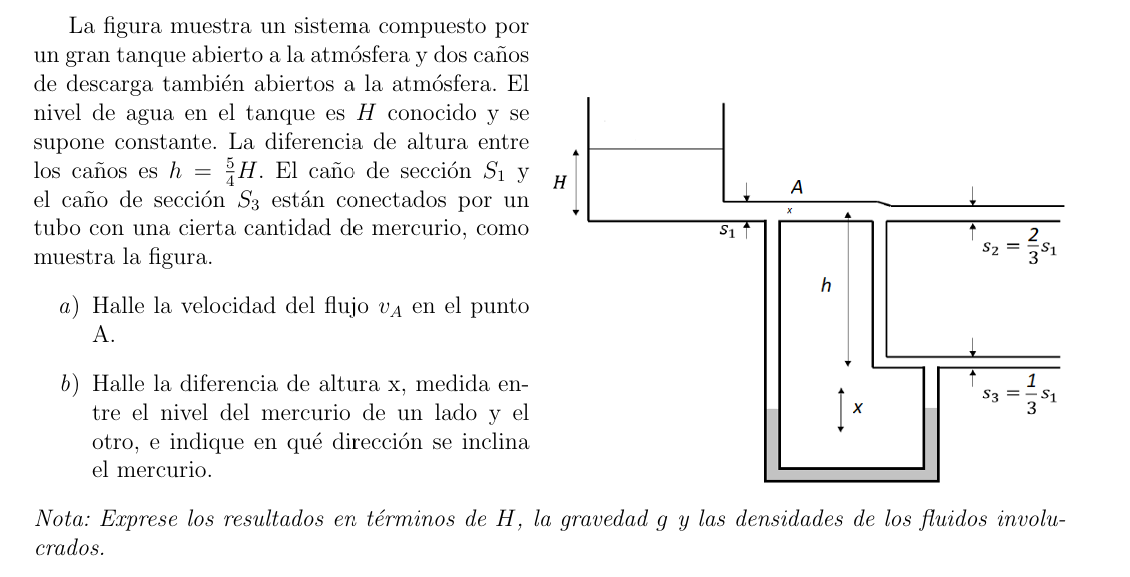
Me planteé el siguiente esquema para poder calcular la diferencia de altura  :
:

Por hidrostática tengo que  y que
y que 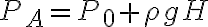 entonces
entonces 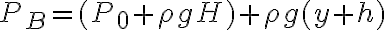
Luego 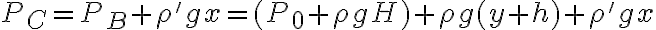 y como la presión debe ser la misma para mismas alturas sé que
y como la presión debe ser la misma para mismas alturas sé que  con
con 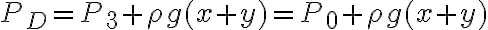
Ese valor para  es negativo ya que densidad de mercurio es mayor a la del agua pero supongo que es porque tomé mal la diferencia de altura y sería mayor en la derecha, pero aún así tampoco es la respuesta.
es negativo ya que densidad de mercurio es mayor a la del agua pero supongo que es porque tomé mal la diferencia de altura y sería mayor en la derecha, pero aún así tampoco es la respuesta.