Holaa, cómo están?
Ya vi la solución subida de este ejercicio pero hay algunas cosas que no me quedaron claras.
Para la parte c iii yo había hecho lo siguiente:
Interpreté que con la def. de velocidad angular, podía hacer la variación del ángulo sobre el tiempo que le llevaba hacerlo. Considerando ángulo inicial y tiempo inicial nulos, me quedó como en la foto. Por qué sería incorrecto? La solución es que tiende a infinito. Eso es porque el movimiento de la "subida" siempre se está repitiendo? Pero cómo hago si quiero hallar cómo lo hace sin considerar ese movimiento en bucle?
Además quería preguntar sobre la "pregunta extra" que se plantea en la solución: "cómo usar una ec que aparece en la solución para hallar el período del movimiento oscilatorio que se da cuando Vo a la dos < 4*(g/R)"
A mí lo que se me ocurriría hacer es multiplicar por 4 el tiempo que demora en llegar a ese ángulo máx. (uno para la subida hasta pi, otro para la bajada, para la subida y bajada del otro lado)... Estaría bien? No sé cómo sería con la ecuación que aparece en la solución.
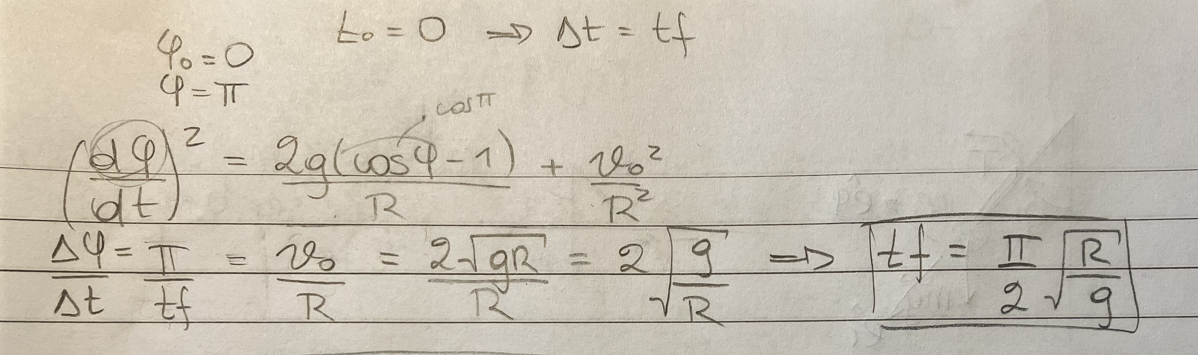
Tampoco entendí en qué momento la normal (ejercida por la barra) ejercería una fuerza en dirección contraria a lo que sería la tensión (ejercida por un hilo). Sería cuando la masa esté arriba y entonces ahí N sería también hacia arriba?
Graciasss, Saludos.