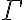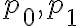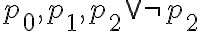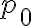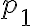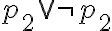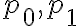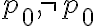Buenas, ¿Cómo están?
Según el diagrama de la diapositiva: 
Es decir, que un conjunto consistente está compuesto por todas sus fórmulas y parte de teoremas.
La consulta es: ¿Cuáles serían esos teoremas? ¿tiene alguna particularidad?
Y por otro lado, si es consistente maximal, ahí sería teoría y entonces ¿contiene a todos los teoremas de PROP?
Espero su respuesta
Gracias!
Saludos
Gonzalo
Hola Gonzalo, un conjunto 
consistente es cualquiera que no derive bottom.
Puede tener algún teorema o no. Por ejemplo estos dos conjuntos son consistentes: {
} y {
}.
El primero no tiene ningún teorema (
y 
son contingencias). El segundo sí tiene el teorema 
.
Además, si un conjunto es consistente, le puedo agregar cualquier teorema que quiera y va a seguir siendo consistente.
Y como vos decís, las teorías contienen siempre a todos los teoremas. En particular, los conjuntos consistentes maximales son teoría, así que también contienen a todos los teoremas.
Saludos,
Juan Diego
Buenas tardes, Juan Diego
Ahora quedó más claro, en realidad puede pasar que no tenga intersección en ese diagrama (como en tu ejemplo, un conjunto de letras proposicionales, que de por sí son contingencias, no tiene intersección con el conjunto de teoremas).
Gracias!
Saludos.-
Exacto. puede tener intersección con los teoremas o no, según cómo sea el conjunto.
Agrego además, porque leyendo mi mensaje anterior capaz que da lugar a confusión:
Hay conjuntos consistentes que sólo tienen contingencias, pero también hay conjuntos inconsistentes que sólo tienen contingencias.
Por ejemplo {
} vimos que tiene sólo contingencias y es consistente.
Pero {
} sólo tiene contingencias, pero es inconsistente.
Saludos,
Juan Diego
Si, entiendo porque por eliminación de la negación se deriva Bottom.
Gracias!
Saludos
Gonzalo
