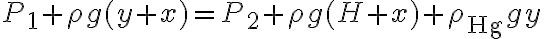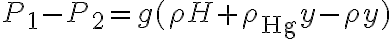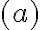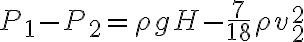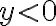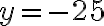Foro de Consultas Ejercicios y Teórico

Buenas! Tengo una duda sobre la parte (3) de este ejercicio:

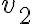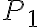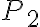A la hora de calcular $v_2$ planteé primero qué relación hay entre $P_1$ y $P_2$ donde, por hidrostática llego a lo siguiente:

$\displaystyle P_1 + \rho g (y+x) = P_2 + \rho g (H+x) + \rho_{\text{Hg}} gy$ de donde llego a $P_1 - P_2 = g(\rho H + \rho_{\text{Hg}}y - \rho y)$ $(a)$

Luego, planteo Bernoulli entre 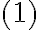$(1)$ y $(2)$ : $\displaystyle P_1 + \frac{1}{2} \rho v_1 ^2 = P_2 + \rho gH + \frac{1}{2}\rho v_2 ^2$ 

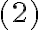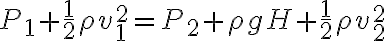
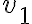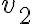Sabiendo que la relación entre $v_1$ y $v_2$ (por parte (1)) es 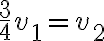$\displaystyle \frac{3}{4} v_1 = v_2$ llego a (por Bernoulli) :

$\displaystyle P_1 - P_2 = \rho gH - \frac{7}{18} \rho v_2 ^2$ $(b)$

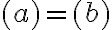$(a) = (b)$ entonces: 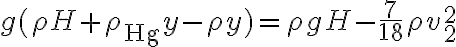$\displaystyle g(\rho H + \rho_{\text{Hg}}y - \rho y) = \rho gH - \frac{7}{18} \rho v_2 ^2$ (se cancelan los términos 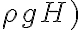$\rho g H)$ , pero llego, en módulo, al resultado exacto pero signo opuesto ya que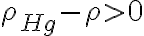 $\rho _{Hg} - \rho > 0$

La solución que plantean es la siguiente:

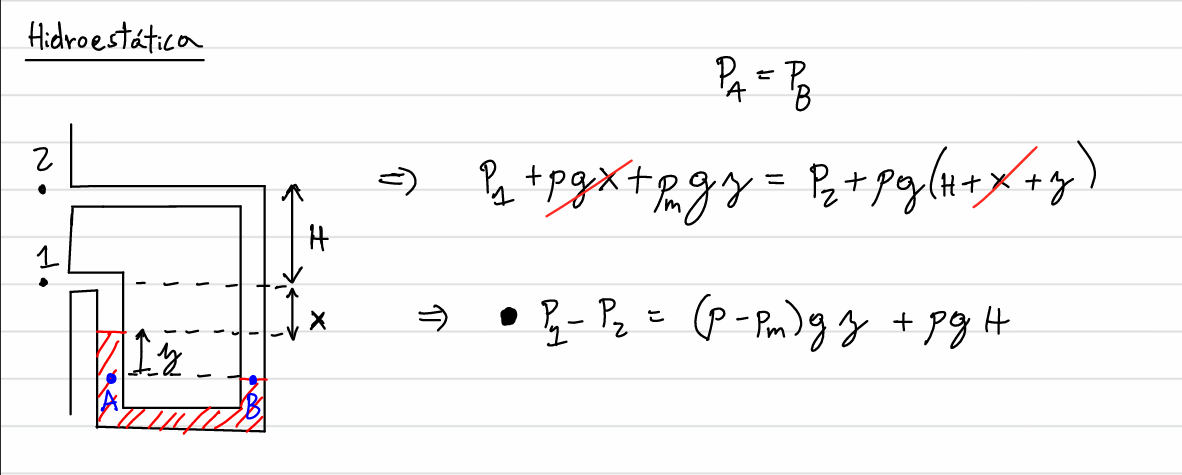
Supongo que mi error está en que consideré la columna de Mercurio tal cual está en la letra del ejercicio pero no entiendo por qué debería de ser como en la segunda forma