Foro Práctico 3

Hola Sebastián.

Un punto 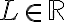$L \in \mathbb{R}$ es punto de aglomeración de una sucesión si existe alguna subsucesión convergente a $L$. Intuitivamente, tu sucesión, va a tener que estar cerca del punto L, para subíndices de la sucesión arbitrariamente grandes (pero no necesariamente a partir de cierto subíndice, ¿se entiende la diferencia?).

En el ejercicio que mencionas, el problema que existe es que si consideras una sucesión cuyo conjunto de puntos de aglomeración sea 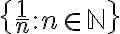$\{\frac{1}{n}: n \in \mathbb{N} \}$ obtendrás que el $0$ también es punto de aglomeración.

Intuitivamente, si tu sucesión va a estar cerca de un punto de la forma 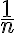$\frac{1}{n}$ para subíndices de la sucesión arbitrariamente grandes, también estará cerca de $0$ para subíndices de la sucesión arbitrariamente grandes (¿se entiende por qué?). Para formalizar esta idea intuitiva podemos hacer una prueba similar a la que hicimos para probar el teorema de B-W en el teórico, si quieres hoy lo vemos en clase.

Saludos, Florencia.