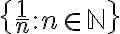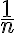¡Hola, buen día! Estuve trabajando en el ejercicio 6, y me surgieron un par de dudas que me gustaría poder aclarar:
Primero, sobre el concepto de punto de aglomeración: lo que entendí es que se trata de encontrar valores hacia los cuales la sucesión "se va acercando" a través de alguna subsucesión, o sea, como que uno puede armar una subsucesión que converge a ese valor. En particular, en los ejemplos de los incisos (a) y (b) me da la sensación de que la idea es ir "dando vueltas" alrededor de ciertos valores, repitiéndolos y cada tanto sumando nuevos, para que aparezcan como puntos de aglomeración.
¿Está bien entendido así? ¿Podría pedirles si me puede dar alguna explicación más intuitiva o algún ejemplo adicional para terminar de afianzar la idea?
Por otro lado, en el inciso (c) se pide pensar si existe una sucesión cuyos puntos de aglomeración sean exactamente los elementos de
A={1n:n∈N}A = \left\{ \frac{1}{n} : n \in \mathbb{N} \right\}A={n1:n∈N}.
Me surgieron dudas fuertes en este apartado, porque cuando lo comenté con la profesora en el teórico del viernes a las 14:30, me mencionó que sería interesante analizar qué pasa con la sucesión acercándose a 0, usando el teorema de Bolzano-Weierstrass en lo que me dijo que sería una prueba que no es fácil de realizar y entender en primera instancia.
Hasta donde llegué, veo que
1n→0\frac{1}{n} \to 0n1→0 cuando
n→∞n \to \inftyn→∞, así que me imagino que, de alguna forma, el 0 podría aparecer como punto de aglomeración, aunque no esté explícitamente en el conjunto A.
¿Es eso lo que pasa? ¿Podría explicarme cómo usar Bolzano-Weierstrass para justificar qué pasa en este caso? Y, en particular, ¿por qué eso afecta a si la sucesión puede tener exactamente como puntos de aglomeración a los del conjunto A y no más?
¡Muchísimas gracias a los que leen por la ayuda y por tomarse el tiempo!