Qué tal Gonzalo?
Muy bien planteada la pregunta, y me parece excelente que hayas identificado que la condición de desprendimiento se obtiene imponiendo que la fuerza normal se anule, y que el ángulo en el cual esto ocurre depende efectivamente de la velocidad inicial. Estos son los dos puntos clave del problema.
En cuanto al inconveniente que mencionás, el problema dimensional probablemente provenga de la expresión que obtuviste para la velocidad angular en la parte b. Fijate que en tu ecuación te quedó un término con la velocidad angular al cuadrado, y lo estás igualando con otro término que tiene dimensiones de velocidad al cuadrado. Eso no es coherente: el cuadrado de una velocidad angular tiene dimensiones diferentes. Corregir eso debería resolver el problema dimensional que estás viendo dentro del argumento del arcos.
Por otro lado, tu estrategia en la parte c está correcta. Con la nueva expresión obtenida en la parte b se obtiene una nuevo argumento para el arcos. Los que se te pide justamente tiene que ver con la existencia (o no) de la solución. Como mencionás, hay que analizar cuándo tiene sentido el argumento del arccos: si el valor que te queda está fuera del dominio de la función (es decir, menor que –1 o mayor que 1). Eso te lleva a una discusión sobre qué pasa cuando la velocidad inicial es muy grande.
Saludos,
Daniel Gau.
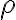y reemplace con lo que halle en la parte b en e
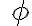para poder dar con en ángulo de desprendimiento y ahí empezar a ver las situaciones según Vo.