Hola! buenas tardes.
El ejercicio lee: 
La sección en particular a la que me quiero referir es: 
Si consideramos la velocidad media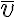 
entre los puntos 3 y 9 del reloj, la velocidad instantánea 
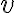en el punto 6 del reloj, y el segmento de recta 
entre los puntos 6 y 12 del reloj:
Mi respuesta es que sí, y lo puedo afirmar porque
* 
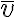apunta directamente hacia el número 9 del reloj, en consecuencia, 
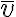resulta perpendicular a
* 
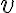en el punto 6 del reloj es tangente al borde del reloj por lo que que resulta perpendicular .
Entonces como ambos vectores son perpendiculares al mismo segmento de recta, son necesariamente paralelos. Por las partes anteriores del ejercicio y dado que el segundero tiene dirección horaria, podemos afirmar que tienen la misma dirección.
Este razonamiento, ¿podría extenderse a cualquier par de puntos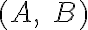 
en el reloj? Más generalmente, ¿esto se puede observar en movimientos "más libres"?
No se si me explico bien. Lo que quiero preguntar es si existe un resultado similar al teorema del valor medio, que te afirme que si la velocidad media entre dos puntos A y B tiene una dirección determinada, entonces existe un punto entre A y B en el cual la velocidad instantánea tiene la misma dirección que la velocidad media.
Quizá es una trivialidad, pero por ejemplo se me ocurre un escenario para el cual no estoy tan seguro de que esto suceda: el movimiento de una pelota que se deja caer desde una altura 
con una velocidad horizontal inicial distinta de cero, que rebota en el piso en un cierto tiempo 
y luego choca contra una pared a altura en un tiempo 
.
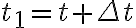En este caso, la velocidad media sería perpendicular al suelo, ¿o me equivoco? En cuyo caso, no visualizo ningun punto en la trayectoria de la pelota para el cual la velocidad instantanea sea perpendicular al suelo también.
Gracias de antemano! Saludos.
Hola Franco,
Vamos respondiendo por partes. Respecto a lo que pregunta el ejercicio 2 parte c, es correcto tu razonamiento al decir que la dirección de la velocidad media entre las posiciones de la aguja del reloj que marcan las 3 y las 9 coincide con la dirección de la velocidad instantánea en 6.
También el ejercicio nos pide cuestionarnos qué pasa entre 3 y 7. ¿Planteaste esta situación? Supongo que sí debido a tu siguiente pregunta. En efecto, en el caso de la aguja del reloj podemos calcular la velocidad media entre dos tiempos y trazando una perpendicular por el origen encontramos un punto de la circunferencia por el cual la tangente (a la que es paralela la velocidad instantánea en ese punto) es paralela a la dirección de dicha velocidad media.
Por otro lado, pensemos en el ejemplo de caída libre que planteas (desde que soltamos al objeto del reposo y toca el suelo). Al ser un movimiento rectilíneo, la dirección de la velocidad media y la velocidad instantánea siempre coinciden (lo que te puede cambiar es el sentido de la velocidad media, dependiendo de los tiempos final e inicial que te interesen). Si planteas que tiene una velocidad inicial con componentes según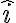
y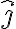 
, tal que rebota en el suelo formando un ángulo respecto a la horizontal y vuelve a chocar contra otra pared. La posición 
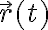no es una función diferenciable en el punto que rebota, por lo que no podes aplicar el teorema del valor medio que sugieres, te recomiendo leer las hipótesis del teorema (aplicable a funciones continuas y diferenciables, es decir, lindas). Podes usar dicho teorema definiendo una función r(t) diferenciable a trozos.
Vamos respondiendo por partes. Respecto a lo que pregunta el ejercicio 2 parte c, es correcto tu razonamiento al decir que la dirección de la velocidad media entre las posiciones de la aguja del reloj que marcan las 3 y las 9 coincide con la dirección de la velocidad instantánea en 6.
También el ejercicio nos pide cuestionarnos qué pasa entre 3 y 7. ¿Planteaste esta situación? Supongo que sí debido a tu siguiente pregunta. En efecto, en el caso de la aguja del reloj podemos calcular la velocidad media entre dos tiempos y trazando una perpendicular por el origen encontramos un punto de la circunferencia por el cual la tangente (a la que es paralela la velocidad instantánea en ese punto) es paralela a la dirección de dicha velocidad media.
Por otro lado, pensemos en el ejemplo de caída libre que planteas (desde que soltamos al objeto del reposo y toca el suelo). Al ser un movimiento rectilíneo, la dirección de la velocidad media y la velocidad instantánea siempre coinciden (lo que te puede cambiar es el sentido de la velocidad media, dependiendo de los tiempos final e inicial que te interesen). Si planteas que tiene una velocidad inicial con componentes según
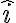y 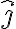, tal que rebota en el suelo formando un ángulo respecto a la horizontal y vuelve a chocar contra otra pared. La posición 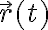no es una función diferenciable en el punto que rebota, por lo que no podes aplicar el teorema del valor medio que sugieres, te recomiendo leer las hipótesis del teorema (aplicable a funciones continuas y diferenciables, es decir, lindas). Podes usar dicho teorema definiendo una función r(t) diferenciable a trozos. Gracias por tu pregunta, espero haya aclarado la situación.
Atentamente,
Lucía