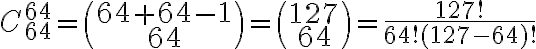Ejercicio 3 práctico 3

Ejercicio 3 práctico 3

de Mateo Roman Allonca Maldonado -
Número de respuestas: 2

Hola, necesito saber si está correcto el razonamiento de este ejercicio. Dice lo siguiente: 

image.png

Además pongo imagen de un tablero para que se entienda mejor: 

tablero de ajedrez

Mi idea es la siguiente: primero contar todos los casos posibles que el rey se pueda mover de a1 hasta h8 (contando también los casos en que se mueve en diagonal)

El tablero cuenta con 64 espacios, por lo tanto sería una combinación con repetición de 64 en 64 

C_{64}^{64} = \binom{64 + 64 - 1}{64} = \binom{127}{64} = \frac{127!}{64!(127 - 64)!}

Luego, se restan los casos en que únicamente el rey se puede mover de forma diagonal. De a1 a h8 hay 7 movimientos, de a2 a g8 hay 6 movimientos, y así hasta llegar hasta a7 a b8 que hay 1 movimiento. Lo mismo para la otra parte del tablero (de la diagonal principal hacia abajo). Entonces sería 7!x6!

Luego serían restar la combinación con la permutación de casos en diagonal. 

Está bien mi análisis? Saludos. 
En respuesta a Mateo Roman Allonca Maldonado

Re: Ejercicio 3 práctico 3

de Guillermo Rivas Nuñez -
No sabría decir si el razonamiento que hiciste fue correcto, pero en el teórico al que voy el profesor puso como ejemplo un ejercicio similar a este de ir de determinado edificio a otro, y el método que nos enseñó fue de tomar la cantidad de movimientos totales que se deberán realizar (en este caso 7 hacia arriba y 7 hacia la derecha) y representarlos como si se tratase de una palabra: DDDDDDDAAAAAAA. Como las D y las A son indistinguibles entre sí, se las toman como repeticiones en una permutación de 14 letras, y el resultado final daría entonces: 14!/(7!7!), lo que suma 3432