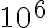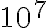Estimadas y estimados:
para compartir las experiencias con los distintos lenguajes en la realización de estos primeros ejercicios del curso, pedimos que cada participante conteste este mensaje, indicando:
- Qué lenguaje utilizó para programar el ejercicio 3.1
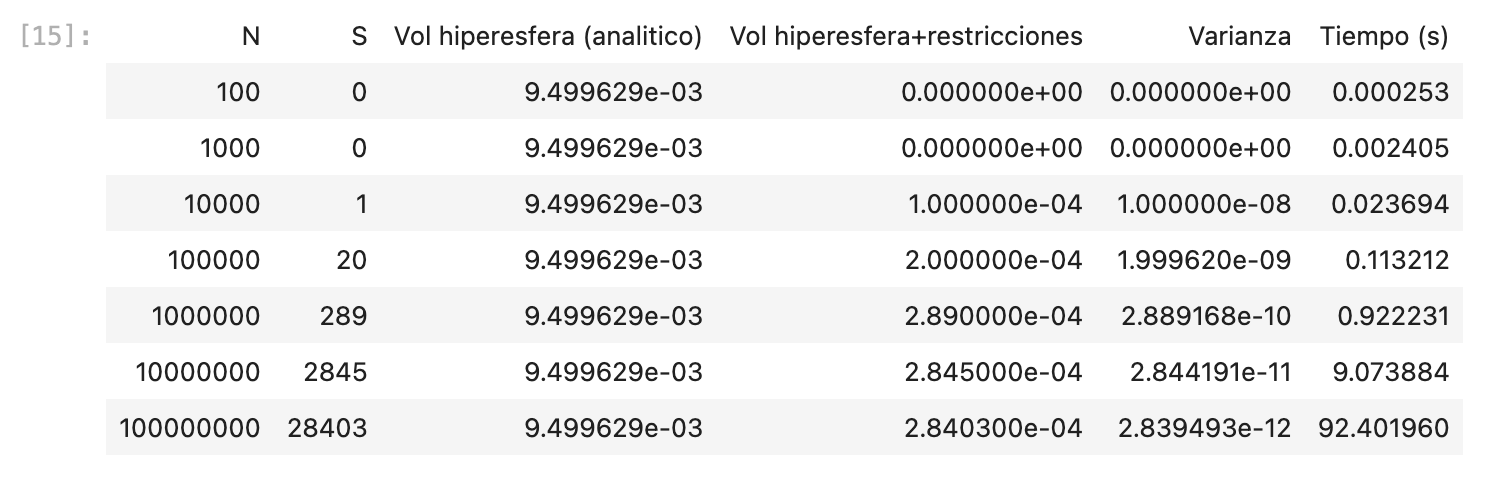
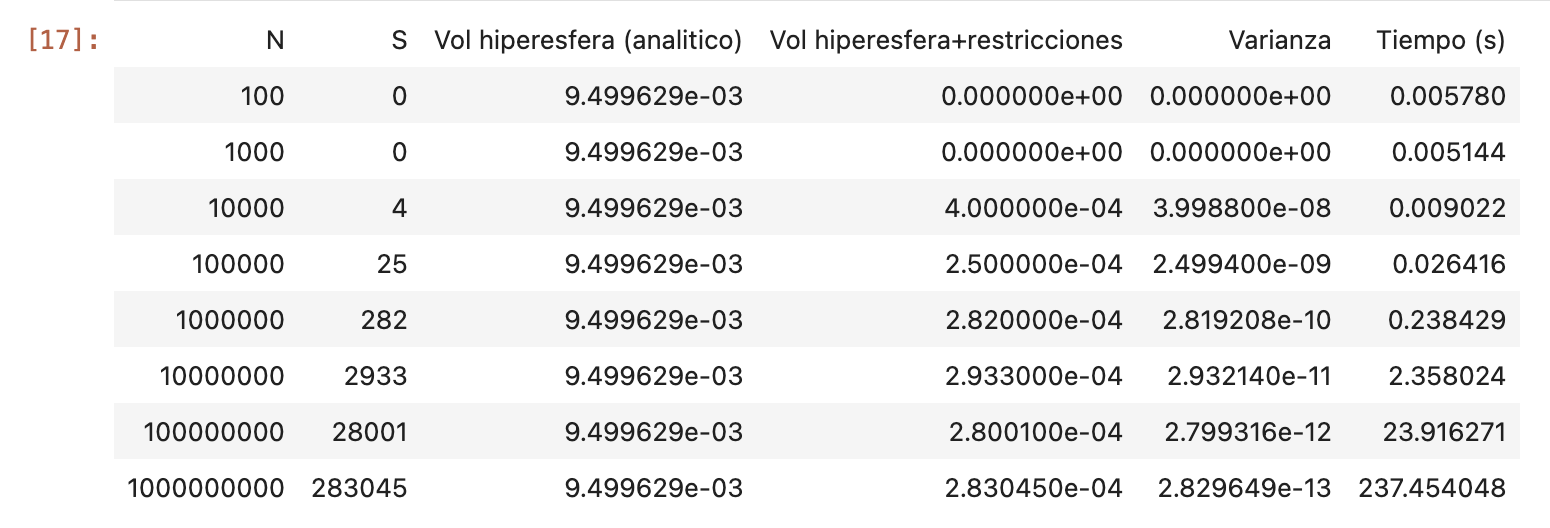
- Qué tiempo de ejecución insumió el programa en la parte a para un tamaño de muestra N=1E+6
- Si realizaron corridas con otros N todavía mayores, y en ese caso cual fue el mayor N que usaron y qué tiempo insumió
- Otros comentarios (problemas de memoria, dificultades con las bibliotecas de números aleatorios, elementos que hicieron sencillo o complicado resolver la tarea).
Muchos saludos
Héctor