Buenas, les paso el código que estuve armando para los diagramas de fase, en particular deje pronto el de la saturación que estuvimos hablando la clase pasada, me parece que es un buen ejemplo para ver bien como usar el código,
import numpy as np
import matplotlib.pyplot as plt
# --- Definir la función de saturación de forma vectorizada ---
def sat(a):
"""
sat(a) = 1 si a > 1
a si |a| <= 1
-1 si a < -1
"""
return np.where(a > 1, 1, np.where(a < -1, -1, a))
def f(x1, x2):
"""
x1' = x2
x2' = x1 - sat(2*x1 + x2)
"""
dx1 = x2
dx2 = x1 - sat(2*x1 + x2)
return dx1, dx2
x1_min, x1_max = -10.0, 10.0
x2_min, x2_max = -10.0, 10.0
n_puntos = 120
x1_vals = np.linspace(x1_min, x1_max, n_puntos)
x2_vals = np.linspace(x2_min, x2_max, n_puntos)
X1, X2 = np.meshgrid(x1_vals, x2_vals)
# Arrays para las derivadas
DX1 = np.zeros_like(X1)
DX2 = np.zeros_like(X2)
for i in range(n_points):
for j in range(n_points):
dx1, dx2 = f(X1[i, j], X2[i, j])
DX1[i, j] = dx1
DX2[i, j] = dx2
plt.figure(figsize=(4, 4))
plt.streamplot(X1, X2, DX1, DX2, density=2.0, arrowsize=1, linewidth=1)
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.xlim([x1_min, x1_max])
plt.ylim([x2_min, x2_max])
plt.xlabel('$x_1$')
plt.ylabel('$x_2$')
plt.title('Diagrama de fase ')
plt.grid(True)
plt.tight_layout()
plt.show()
Usa dos bibliotecas, numpy (que es usada para mandar calculos de arreglos, matrices y eso) y matplotlib (esta es mas importante porque la vamos a usar para los diagramas de fase) que contiene la función plt.streamplot que vamos a usar para los diagramas de fase.
En la primera parte del código te definís la función que quieras usar, yo ahí metí la funcion sat, que como no esta en numpy la tuve que hacer a mano, si quieren meter otra tipo sen(xy) se puede meter tal cual, porque numpy la tiene definida. Después que hacen eso la cargan en f(x,y).
La siguiente parte:
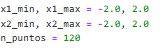
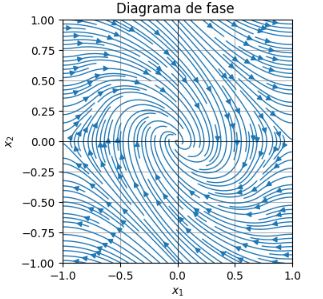
Sirve para definirte los limites de la imagen, por ejemplo si quieren ver mejor el comportamiento del origen ponen un intervalo pequeño:
Si quieren ver un comportamiento mas global, agrandan el los x_max y x_min:
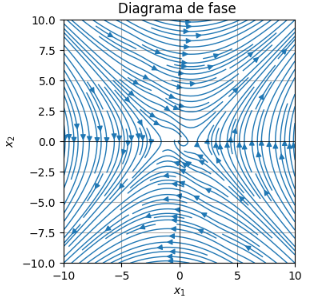
Ahí pueden ver lo que charlamos en clase, el origen es asintóticamente estable, pero solo sucede localmente, porque agrandando vemos como hay regiones que son inestables. Después, si quieren pueden aumentar la densidad de lineas o disminuirla tocan el density de esta función
plt.streamplot(X1, X2, DX1, DX2, density=2.0, arrowsize=1, linewidth=1)
Después lo demás son cosas de plot y eso, que sirven para visualizarlo, una cosa que está buena mirar es la cuestión el mershgrind y como funcionan los diagramas de flujo : Plot Phase portraits of dynamical systems and state-space models in python , ahí encontré este video que lo explican re bien y con bastante detalle, igual ya sería una cuestión de métodos numéricos, no es necesario para plotear.
Hice el programa en Conda, pero en google colab debería de andar bien, cualquier duda estoy a las ordenes!
Saludos
