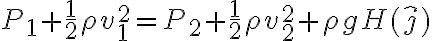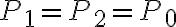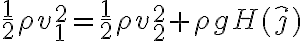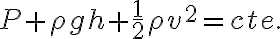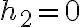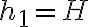Foro de Consultas Ejercicios y Teórico

Buenas! Tengo una duda puntual sobre este ejercicio:

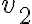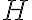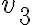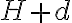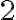Para poder determinar las velocidades a las que sale el agua por los orificios (sean $\displaystyle v_2$ la velocidad con la que sale el agua por el orificio a distancia $H$ desde la parte de más arriba, y $\displaystyle v_3$ la que se encuentra a distancia $\displaystyle H+d$) hice, primero, Bernoulii entre un punto en la superficie, $1$, y $2$ el primer orificio. Entonces:

 $\displaystyle P_1 + \frac{1}{2}\rho v_1^2 = P_2 +\frac{1}{2}\rho v_2^2 + \rho gH(\hat{j})$  pero sé que $\displaystyle P_1 = P_2 = P_0$ entonces $\displaystyle \frac{1}{2}\rho v_1^2 = \frac{1}{2}\rho v_2^2 + \rho g H(\hat{j})$

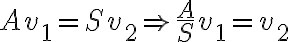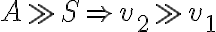Por CONTINUIDAD: $\displaystyle Av_1 = Sv_2 \Rightarrow \frac{A}{S}v_1=v_2$  (donde $A$ es el área de la parte abierta) y como se tiene que $\displaystyle A \gg S \Rightarrow v_2 \gg v_1$ por lo que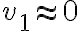 $\displaystyle v_1 \approx 0$ 

Luego : 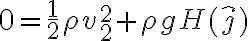$\displaystyle 0= \frac{1}{2}\rho v_2 ^2 + \rho g H(\hat{j})$ pero mi duda es cómo tomarme el signo del término potencial gravitatoria porque, si elijo 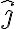$\hat{j}$ para abajo sería 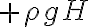$\displaystyle +\rho g H$ y no tendría sentido a la hora de despejar 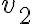$v_2$ porque me quedaría raíz negativa, pero si elijo el versor positivo hacia arriba sí logro llegar a un resultado coherente para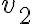 $v_2$ 

¿Tengo que elegir 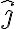$\hat{j}$ si o si para arriba?

(Por las dudas me tomé el cero en la superficie de arriba)