Foro de consultas

Buenas,
La definición de proceso estacionario es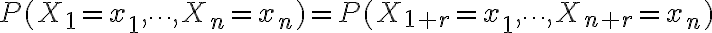
$P(X_{1} =x_{1},\cdots , X_{n}=x_{n})=P(X_{1+r} =x_{1}, \cdots , X_{n+r} =x_{n})$ para todo 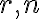$r,n$ y todo $x_{1}, \cdots , x_{n} \in X$.

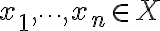Sin embargo considero difícil demostrar si que 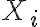${X_{i}}$ es estacionario por este lado. Lo que hice fue suponer que es estacionario y encontrar la distribución estacionaria 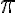$\pi$ tal que 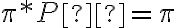$\pi*P  = \pi$. Entiendo que esto demuestra que es estacionaria si y solo si nos encontramos en el caso de que justamente la primera distribución coincida con este 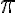$\pi$ encontrado (lo cual sucede porque 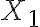$X_{1}$ es uniformemente distribuida).
Esta bien este razonamiento? Debería ser capaz de demostrarlo con la definición?

Además, en la parte b), utilice justamente que es estacionario para poder usar la fórmula de las diapositivas: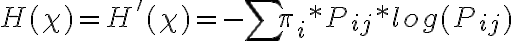 
$H( \chi )=H'( \chi ) = -\sum {\pi_{i}*P_{ij}*log(P_{ij}) }$
No sé si es lo esperado, o si se prefiere que se consiga demostrar mediante la aplicación de la definición nomas?
Saludos!