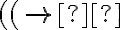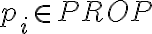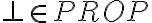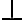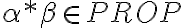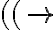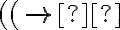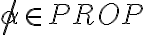Hola Diego,
se puede demostrar que un elemento no pertenece a un conjunto inductivo de varias formas, vos mencionás dos de esas formas. Te comento para cada una de las formas que mencionás cómo debería ser la demostración para que quede completa.
Mostrando que el elemento no se puede construir usando ninguna de las reglas del conjunto inductivo
se puede demostrar que un elemento no pertenece a un conjunto inductivo de varias formas, vos mencionás dos de esas formas. Te comento para cada una de las formas que mencionás cómo debería ser la demostración para que quede completa.
Mostrando que el elemento no se puede construir usando ninguna de las reglas del conjunto inductivo
Acá diríamos que:
Acá se debería definir una propiedad que cumplan todos los elementos de 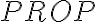 , por ejemplo que todas las fórmulas de
, por ejemplo que todas las fórmulas de 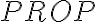 tienen igual cantidad de paréntesis que abren que de paréntesis que cierran.
tienen igual cantidad de paréntesis que abren que de paréntesis que cierran.
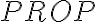 , por ejemplo que todas las fórmulas de
, por ejemplo que todas las fórmulas de 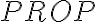 tienen igual cantidad de paréntesis que abren que de paréntesis que cierran.
tienen igual cantidad de paréntesis que abren que de paréntesis que cierran.Luego se prueba la propiedad definida usando el PIP para 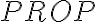 , de forma de asegurarnos que efectivamente todas las fórmulas de
, de forma de asegurarnos que efectivamente todas las fórmulas de 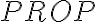 cumplen la propiedad.
cumplen la propiedad.
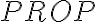 , de forma de asegurarnos que efectivamente todas las fórmulas de
, de forma de asegurarnos que efectivamente todas las fórmulas de 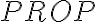 cumplen la propiedad.
cumplen la propiedad. Finalmente podemos mostrar que el elemento 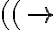 no está en
no está en 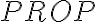 porque no tiene igual cantidad de paréntesis que abren que de paréntesis que cierran.
porque no tiene igual cantidad de paréntesis que abren que de paréntesis que cierran.
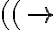 no está en
no está en 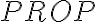 porque no tiene igual cantidad de paréntesis que abren que de paréntesis que cierran.
porque no tiene igual cantidad de paréntesis que abren que de paréntesis que cierran.Cualquier otra duda a las órdenes!