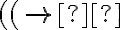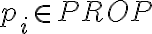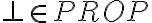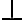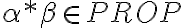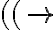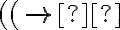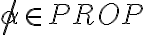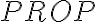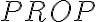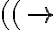buenas, siempre me genera dudas el probar que algo no pertenece a un conjunto inductivo, porque para probar que algo si pertenece es algo muy formal, das todos los pasos para llegar al elemento que queres probar que pertenece y ta, pero para probar que algo no pertenece es una demostracion mas personal no?
por ejemplo: ¿podria decir que una manera de probar que ((-> no pertenece es decir que todos los elementos de prop son construidos a partir de las reglas base y que no hay manera de construir ((-> a partir de estas reglas ya que ninguno de los elementos dados por esas reglas base se encuentran en esa palabra, cosa que deberia pasar si perteneciese debido a las reglas inductivas?
y podria decir que otra manera de demostrar que no pertenece es que la utilizacion de un conector implica 2 partes y parentesis a los lados, cosa que no cumple la palabra?
estan bien esas demostraciones asi escritas o habria que hacerlo de una manera mas formal, identificando y probando por induccion una propiedad que cumplan todos los elementos del conjunto y ver que el elemento no la cumple?
saludos