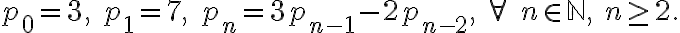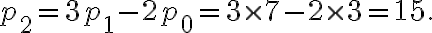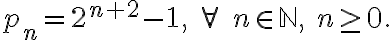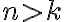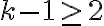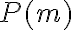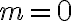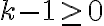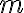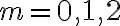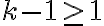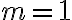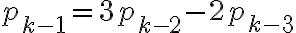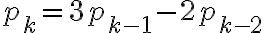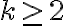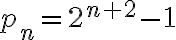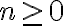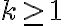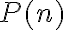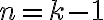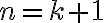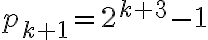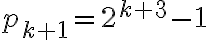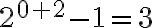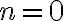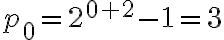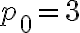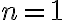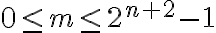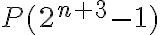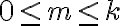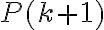Les dejo el siguiente ejercicio para practicar el principio de inducción fuerte. Intenten hacerlo y lo comentamos en esta entrada del foro.
Ejercicio:
Después de transcurrir  meses en un experimento de invernadero, el número
meses en un experimento de invernadero, el número 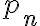 de plantas (de un tipo particular) satisface las siguientes ecuaciones:
de plantas (de un tipo particular) satisface las siguientes ecuaciones:
Por ejemplo, tomando 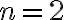 en la expresión anterior, se obtiene la cantidad de plantas en el segundo mes del experimento:
en la expresión anterior, se obtiene la cantidad de plantas en el segundo mes del experimento:
Probar que la cantidad de plantas 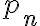 , en el mes número
, en el mes número  del experimento, está dada por:
del experimento, está dada por:
Sugerencia: usar el principio de inducción fuerte.