En el ejercicio de la distancia de la recta con el plano, no hay que confirmar que la recta sea paralela al plano? Pregunto porque si la recta intersecta al plano la distancia sería 0 y estaría mal la respuesta.
En respuesta a Miranda Faustina De Gregorio Acosta
Re: Ejercicio del examen febrero
Yo tengo la misma duda, en la corrección aparece el vector como (1,-2,-1) pero en la hoja impresa yo recuerdo haber visto (1,-1,-1).
Con el vector (1,-2,-1) la recta es paralela al plano, pero con el vector (1, -1, -1) intersecta y la distancia es cero.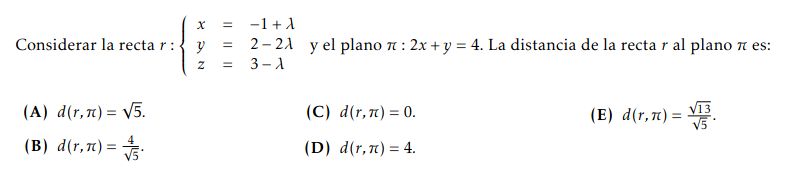
En respuesta a Alvaro Adhemar Kuolas Blanco
Re: Ejercicio del examen febrero
de Germán Sacco Zunino -
Me sumo a la cuestión
Hola,
la letra del ejercicio es la que adjuntaron en este mensaje. La dirección de la recta r está dada por el vector (1,-2,-1) y la dirección normal al plano es(2,1,0). En la solución se aclara que el producto escalar entre estos vectores da cero, por lo tanto son perpendiculares, lo que implica que la recta y el plano son paralelos. Luego se usa la fórmula para hallar la distancia.
Saludos
la letra del ejercicio es la que adjuntaron en este mensaje. La dirección de la recta r está dada por el vector (1,-2,-1) y la dirección normal al plano es(2,1,0). En la solución se aclara que el producto escalar entre estos vectores da cero, por lo tanto son perpendiculares, lo que implica que la recta y el plano son paralelos. Luego se usa la fórmula para hallar la distancia.
Saludos
El problema es que en la hoja impresa entregada en el examen el vector es (1, -1, -1), difiere a la corrección.
¿Pueden verificar que las hojas impresas (en todas sus versiones) cual es el vector director de la recta?
¿Pueden verificar que las hojas impresas (en todas sus versiones) cual es el vector director de la recta?
