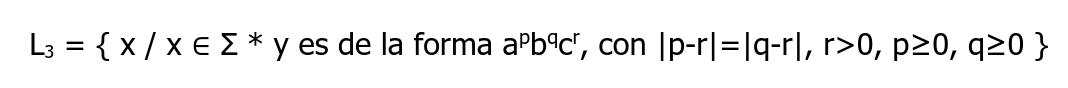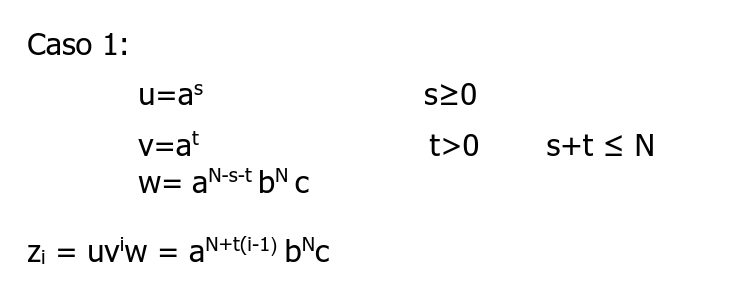Hola, estuve trabajando en la parte a del ejercicio 3 donde se hace pumping lema para poder demostrar que el lenguaje no es regular. A la hora de resolverlo me enfrente a una duda en cuanto al largo de v para las diferentes familias ya que pueden haber tiras con p,q = 0. En la solución se trabaja con solo una familia la cual se le pone la restricción de que la cantidad de a's es mayor a 0.
Como es el razonamiento aquí, por qué asume que la cantidad de a's en ese caso es mayor a 1, satisface la restricción del pumping lema pero no se estaría considerando el caso en que p = q = 0?