Buenos días.
Mi consulta es por la serie que adjunto foto. Según las respuestas la serie converge. Apliqué el criterio del cociente y me quedó lo último que se ve. Mi pregunta es: ¿Dentro de un criterio, es decir mientras vamos desarrollando el mismo, es posible aplicar otro criterio? ¿O es necesario finalizar el mismo, por ejemplo, en el caso del cociente que nos dé un limite finito?
En el caso adjunto, se nos ocurría usar infinitesimales para decir que "lo de arriba" tiende más lento que "lo de abajo" a infinito, por lo que nos resultaba 0. Entonces por criterio del cociente nos da un L<1 por lo tanto Converge ¿Es correcto?
Link del parcial: https://eva.fing.edu.uy/mod/resource/view.php?id=184665
Gracias por leer. Saludos.
En respuesta a Lucas Martin Ruiz Pecora
Re: 1er. Parcial Segundo Sem. 2022 -Series
de Mateo Musitelli -
Hola Lucas, ¿cómo estás?
Mezclar criterios de clasificación de series en una misma aplicación no es un procedimiento acertado.
No me queda claro qué criterios de clasificación estás aplicando de manera "anidada", pero con lo que refieres a "infinitesimales" no identifico a un criterio de los trabajados en el curso.
¿Me clarificarías?
Quedo atento,
M
Mezclar criterios de clasificación de series en una misma aplicación no es un procedimiento acertado.
No me queda claro qué criterios de clasificación estás aplicando de manera "anidada", pero con lo que refieres a "infinitesimales" no identifico a un criterio de los trabajados en el curso.
¿Me clarificarías?
Quedo atento,
M
En respuesta a Mateo Musitelli
Re: 1er. Parcial Segundo Sem. 2022 -Series
Buenas.
No lo mencioné. A mitad del criterio del cociente, cuando nos queda lo último, pensaba aplicar el criterio de comparación. Pero si no es correcto veré por dónde ir. Con lo de infinitesimales no me refería a un criterio, sino simplemente ver si podíamos decir que se asemeja a 1/n (tal vez me estoy mezclando con el criterio de equivalentes). No sé si me podrías brindar alguna pista para cómo encarar este ejercicio desde cero ignorando lo que hice.
Como tenía el "n!" Supuse que se realizaba con criterio del cociente.
Saludos.
En respuesta a Lucas Martin Ruiz Pecora
Re: 1er. Parcial Segundo Sem. 2022 -Series
de Mateo Musitelli -
Lucas:
Gracias por la aclaración. Efectivamente, la anidación que referís (vuelvo a destacar) es incorrecta.
La forma de proceder (debido al factorial y al producto de los logaritmos) es utilizando el criterio del cociente, puesto que se simplifican muchos términos.
Te pido que plantees tu el criterio, notando la repetición en el numerador y el denominador de muchos términos:
Teniendo en cuenta los términos cancelados y el límite con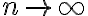
, deberías pdoer determinar la conclusión del criterio.
Quedo atento a tu avance,
M
Gracias por la aclaración. Efectivamente, la anidación que referís (vuelvo a destacar) es incorrecta.
La forma de proceder (debido al factorial y al producto de los logaritmos) es utilizando el criterio del cociente, puesto que se simplifican muchos términos.
Te pido que plantees tu el criterio, notando la repetición en el numerador y el denominador de muchos términos:
Teniendo en cuenta los términos cancelados y el límite con
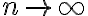, deberías pdoer determinar la conclusión del criterio.Quedo atento a tu avance,
M