Hola Martín. Vimos en el curso que la solución general de una recurrencia homogénea de grado 2 cuyo polinomio característico tiene raices reales distintas 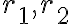 es siempre de la forma
es siempre de la forma 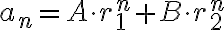 con
con 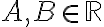 . En el caso del ejercicio (todas las versiones) las raíces serían
. En el caso del ejercicio (todas las versiones) las raíces serían 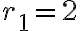 y
y 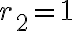 . En el caso concreto de tu versión
. En el caso concreto de tu versión 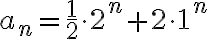 , el polinomio característico sería
, el polinomio característico sería 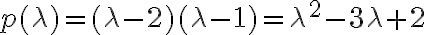 , la recurrencia que verifica la sucesión explícitamente sería
, la recurrencia que verifica la sucesión explícitamente sería 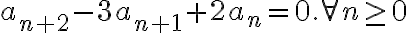 .
.
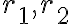 es siempre de la forma
es siempre de la forma 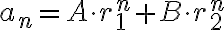 con
con 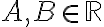 . En el caso del ejercicio (todas las versiones) las raíces serían
. En el caso del ejercicio (todas las versiones) las raíces serían 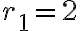 y
y 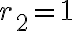 . En el caso concreto de tu versión
. En el caso concreto de tu versión 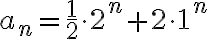 , el polinomio característico sería
, el polinomio característico sería 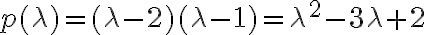 , la recurrencia que verifica la sucesión explícitamente sería
, la recurrencia que verifica la sucesión explícitamente sería 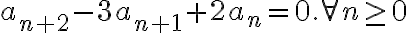 .
.