Buenas,
¿Podrían desarrollar por qué a_n = 2^(n-1) + 2 verifica una relación de recurrencia homogénea de grado 2?
Gracias,
Martín.
Buenas,
¿Podrían desarrollar por qué a_n = 2^(n-1) + 2 verifica una relación de recurrencia homogénea de grado 2?
Gracias,
Martín.
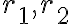 es siempre de la forma
es siempre de la forma 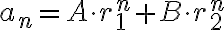 con
con 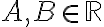 . En el caso del ejercicio (todas las versiones) las raíces serían
. En el caso del ejercicio (todas las versiones) las raíces serían 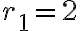 y
y 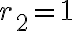 . En el caso concreto de tu versión
. En el caso concreto de tu versión 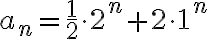 , el polinomio característico sería
, el polinomio característico sería 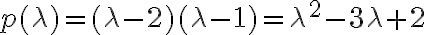 , la recurrencia que verifica la sucesión explícitamente sería
, la recurrencia que verifica la sucesión explícitamente sería 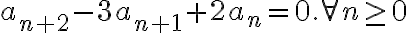 .
.