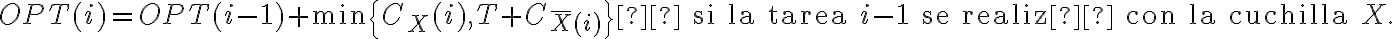Prog3: Segundo Parcial. Acerca de una solución incorrecta del ejercicio 1

Hola.

Ampliamos acá la explicación que está en la solución de uno de los errores detectados en el ejercicio 1.

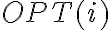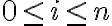En esa solución propuesta $OPT(i)$ , con $0 \leq i \leq n$ , es el costo mínimo para procesar desde la tarea 1 hasta la 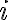$i$ , dado que inicialmente la máquina tiene instalada la cuchilla $A$ .

$OPT(0) = 0,$

$OPT(i) = OPT(i-1) + \min\{ C_X(i), T + C_{\overline{X}(i)} \} \text{ si la tarea } i-1 \text{ se realizó con la cuchilla } X.$

Se toma 0 como caso base (también se puede elegir 1), en el que no hay costo porque no hay materiales a procesar.

En el caso genérico, 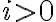$i > 0$ tareas, 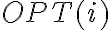$OPT(i)$ es el resultado de sumar al costo mínimo de las 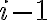$i-1$ tareas anteriores, 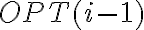$OPT(i-1)$ , el menor costo producido por las dos opciones posibles, que son mantener la misma cuchilla que se usó en la tarea anterior, con costo 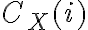$C_X(i)$ , o cambiar de cuchilla con un costo 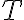$T$ y procesar el material con costo $C_{\overline{X}}(i)$ .

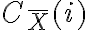Lo valorable de esta propuesta es que se define que significa 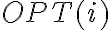$OPT(i)$ , se plantea el caso base, se resuelve el caso genérico en función de casos que involucran menos tareas, y se explica cada término, y por qué las expresiones son correctas.

Un primer inconveniente es que en la recurrencia no se mantiene cuál es la cuchilla usada en la tarea anterior. Por eso es que se necesita una segunda dimensión en la estructura de subproblemas, lo que se expresaría con un segundo parámetro, 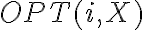$OPT(i,X)$ .

Pero aun si en el algoritmo se resuelve esto manteniendo en una variable cuál es la cuchilla usada, no se obtiene el resultado correcto.

Para verlo, repetimos el ejemplo que está en la solución. Suponemos que $T=5$ y que los costos de cortar cada material con cada cuchilla son


i	1	2
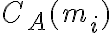$C_A(m_i)$	10	10
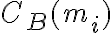$C_B(m_i)$	1	100

En la siguiente tabla vemos cuáles son los costos de todas las posibles elecciones de cuchillas.


Cuchillas	Costo
AA	20
AB	115
BA	21
BB	106

Por inspección, vemos que el costo mínimo ocurre cuando ambas tareas se realizan con la cuchilla

$A$ , producto de sumar 10 por cada tarea y sin costos por cambio de cuchilla.

Ahora veamos que es lo que se obtiene con la recurrencia propuesta


i	1	2
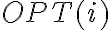$OPT(i)$	6	21

Para

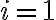$i=1$ el costo es 6, producto de cambiar la cuchilla y procesar el material

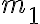$m_1$ con la cuchilla

$B$ . El costo de mantener la cuchilla

$A$ habría sido 10.

Para 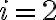$i=2$ el costo es 21, producto de cambiar la cuchilla nuevamente y procesar el material 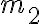$m_2$ con la cuchilla $A$ . El costo de mantener la cuchilla $B$ habría sido 106.

Entonces comprobamos que esta propuesta no siempre encuentra una solución óptima.

El error es esta propuesta, más allá de no encontrar la solución correcta, es que se podría haber notado que esta es una estrategia Greedy. En cada paso se elige lo que localmente, hasta ese paso, es mejor, sin tener en cuenta los efectos de la decisión tomada. En este caso elegir cambiar de cuchilla en la tarea 1, (decisión correcta si no hubiera más tareas) obliga a volver a cambiar de cuchilla en la tarea 2.

Se debe notar que en la misma recorrida en que se calculan los valores óptimos se podría haber construido la solución. Esto no es lo que pasa en los algoritmos de Programación Dinámica, en los que el valor óptimo se calcula en una recorrida, yendo desde los casos base hacia los casos que involucran más elementos, y es en una segunda recorrida, usando los valores óptimos ya calculados, y en el sentido puesto a la recorrida anterior, donde se puede construir la solución.

Saludos