Buenas!
Viendo lo que planteaste, obtuviste un sistema de ecuaciones bastante similar al correcto, a diferencia de algunos factores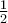 o
o 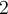 . Estos surgen de tener cierto cuidado al vincular velocidades/aceleraciones tangenciales y respecto del centro de masa.
. Estos surgen de tener cierto cuidado al vincular velocidades/aceleraciones tangenciales y respecto del centro de masa.
Veamos como queda el sistema
Primera elijo positivo hacia la derecha y entrante
Para el cuerpo 1 (el de la izquierda):



Para el cuerpo 2(el que cuelga):

Como ves, planteé positivo hacía abajo del cuerpo dos, y puse la aceleración positiva del cuerpo dos hacia abajo. Esto es coherente ya que en el cuerpo 1 puse positivo hacia la derecha, que corresponde positivo hacia abajo en el cuerpo dos (esto del vínculo entre sus aceleraciones). Además, la aceleración del cuerpo 2 la podríamos llamar también
la podríamos llamar también  ya que corresponde a la parte tangencial del disco. Después
ya que corresponde a la parte tangencial del disco. Después  , esto ya que si planteamos que
, esto ya que si planteamos que  y
y  . Finalmente
. Finalmente 
Veamos ahora el cuerpo 3 (los discos):



Finalmente, el sistema que hay que resolver es:




De aquí en adelante es "solamente" resolver el sistema (podes empezar por sumar la primera y segunda ecuación, sustituir en la última, y esto en la tercera)
Saludos!
Viendo lo que planteaste, obtuviste un sistema de ecuaciones bastante similar al correcto, a diferencia de algunos factores
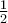 o
o 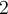 . Estos surgen de tener cierto cuidado al vincular velocidades/aceleraciones tangenciales y respecto del centro de masa.
. Estos surgen de tener cierto cuidado al vincular velocidades/aceleraciones tangenciales y respecto del centro de masa.Veamos como queda el sistema
Primera elijo positivo hacia la derecha y entrante
Para el cuerpo 1 (el de la izquierda):



Para el cuerpo 2(el que cuelga):

Como ves, planteé positivo hacía abajo del cuerpo dos, y puse la aceleración positiva del cuerpo dos hacia abajo. Esto es coherente ya que en el cuerpo 1 puse positivo hacia la derecha, que corresponde positivo hacia abajo en el cuerpo dos (esto del vínculo entre sus aceleraciones). Además, la aceleración del cuerpo 2
 la podríamos llamar también
la podríamos llamar también  ya que corresponde a la parte tangencial del disco. Después
ya que corresponde a la parte tangencial del disco. Después  , esto ya que si planteamos que
, esto ya que si planteamos que  y
y  . Finalmente
. Finalmente 
Veamos ahora el cuerpo 3 (los discos):



Finalmente, el sistema que hay que resolver es:




De aquí en adelante es "solamente" resolver el sistema (podes empezar por sumar la primera y segunda ecuación, sustituir en la última, y esto en la tercera)
Saludos!
