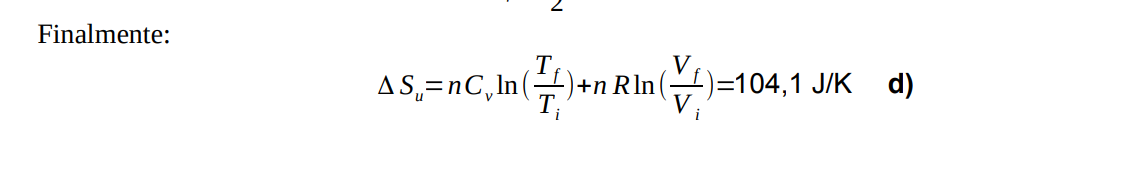Ejercicio 2, parcial noviembre 2023.

Ejercicio 2, parcial noviembre 2023.

de Alejo Suárez Cabezas -
Número de respuestas: 2

Buenos días, tengo una consulta sobre la parte d de este ejercicio. En esta pide encontrar la variacón de energía del universo y en la solución lo pone así:
Lo que no entiendo es la primera parte, la que tiene las temperaturas. Me parece que el resto, la parte con los volúmenes, es la variación de entropía del sistema, entonces supongo que lo primero es la variación de entropía del entorno, pero no sé como llegar a esa expresión. Además es un sistema adiabático así que la entropía del entorno no cambiaría, ¿o sÍ? Gracias.
En respuesta a Alejo Suárez Cabezas

Re: Ejercicio 2, parcial noviembre 2023.

de Ezequiel Maximiliano Amorin Camacho -
Buenas, espero te encuentres bien.
Por la letra del ejercicio, si tomamos nuestro sistema como todo el contenedor, entonces la variación de entropía del resto del universo es cero (pues el contenedor no transfiere energía hacia el exterior). Por otro lado, la variación de entropía del sistema en sí mismo se puede dividir en dos partes: la parte en que aumenta la temperatura (antes de romper la membrana) y la parte en que la membrana está rota y hay expansión libre hasta llenar el contenedor. De ahí, resolviendo \int_{i}^{f} \frac{dQ}{T}, se obtienen las ecuaciones. En el primer caso, se obtiene que la temperatura varía, mientras que V permanece constante. Por otro lado, tras el instante f', el volumen cambia. En cada caso, utilizando las relaciones entre trabajo y calor, y la ley de los gases ideales, se puede llegar a esas expresiones. Espero que esto te ayude.
Saludos!