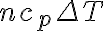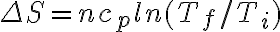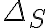Buenas noches, escribo para consultar sobre una duda teórica que surge de este ejercicio.
Mi duda es: A la hora de calcular la entropía utilizando la ecuación que se deduce del primer principio de la termodinámica, en el termino nCvln(Tf/Ti), que sale de integrar nCv.dT/T, ¿por qué se utiliza Cv y no Cp si la variación de energía se da a presión constante?
En los cálculos de este ejercicio al calcular ΔS = nRln(Vf/Vi) + nCvln(Tf/Ti) me da 38.4 J/K, en el apartado de resultados dice que es 39.5 J/K. Calcule el numero de moles usando los datos iniciales, la temperatura final usando la definición de calor específico y el volumen final con la relación entre temperaturas y volúmenes a presión constante. Suponiendo que las cuentas estén bien me gustaría saber si es correcto este procedimiento y la diferencias entre mi resultado y el que nos dan es cuestión de cifras significativas o si me faltó algo.
Por último está el asunto de la variación de la entropía del universo. Dado que no hay intercambio de calor, supuse que esta se debía únicamente al trabajo que el pistón realiza sobre el aire del ambiente, no se si es correcto, pero si lo fuera, ¿como se calcularía? ¿Equivaldría a la entropía debido al trabajo que el gas interno realiza sobre el pistón?
Estas eran mis dudas. Muchas gracias y saludos.