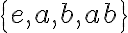Buenas! Espero se encuentren bien.
El ejercicio es el siguiente
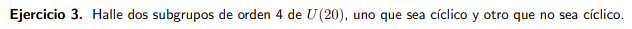
Logré encontrar un subgrupo cíclico a prueba y error pero no logro encontrar uno que no sea cíclico. Tengo que verificar que no haya un elemento generador del grupo, que tenga al neutro, que los inversos estén incluidos y que sea cerrado por multiplicación, pero siempre alguno de estos requisitos me falla.
Hay alguna forma de hacer esto de forma más sistemática?
Muchas gracias!
Saludos,
Diego Furrer