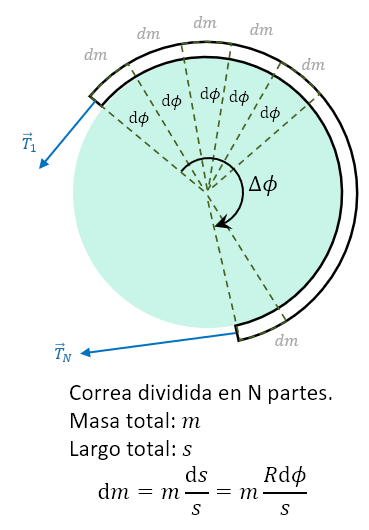
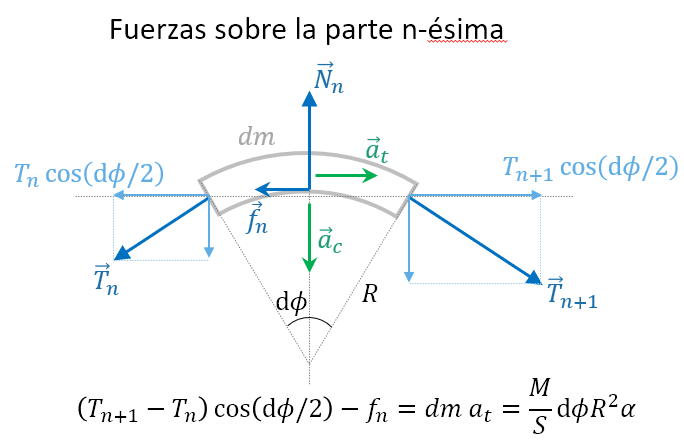
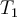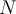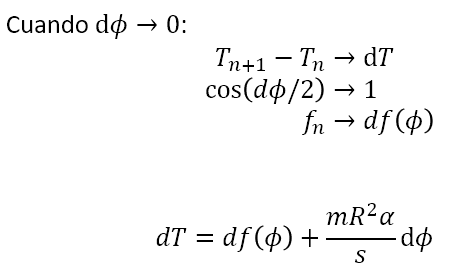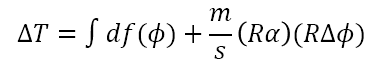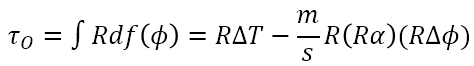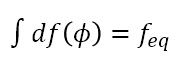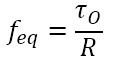Buenas, Diego. Hay que aclarar que el torque que ejerce la correa se debe a la fuerza de rozamiento entre esta y el cilindro. Cuando la correa pasa alrededor de la superficie, al entrar en contacto aparece una fricción distribuida entre sus diferentes puntos. No aparece separadamente un "torque debido a la correa" y "un torque debido a la fricción": son la misma cosa.
La tensión en la correa no es siempre del mismo módulo. Debido al contacto con la superficie, el valor va cambiando progresivamente, en función de la posición y de la fricción. Al final, la tensión en los extremos de la correa es diferente, con lo cual es capaz de ejercer un torque externo no nulo sobre el sistema.
Se puede ver que el efecto neto de esta interacción equivaldría a la aplicación de una única fuerza en la superficie del cilindro que genere el mismo torque. Mi interpretación es que en la última pregunta hay que contestar el valor de esta fuerza equivalente. Igual no le daría demasiadas vueltas ya que, en definitiva, la única operación que tiene sentido dimensional hacer para hallar una fuerza es dividir el torque entre el radio.
Saludos,
NC

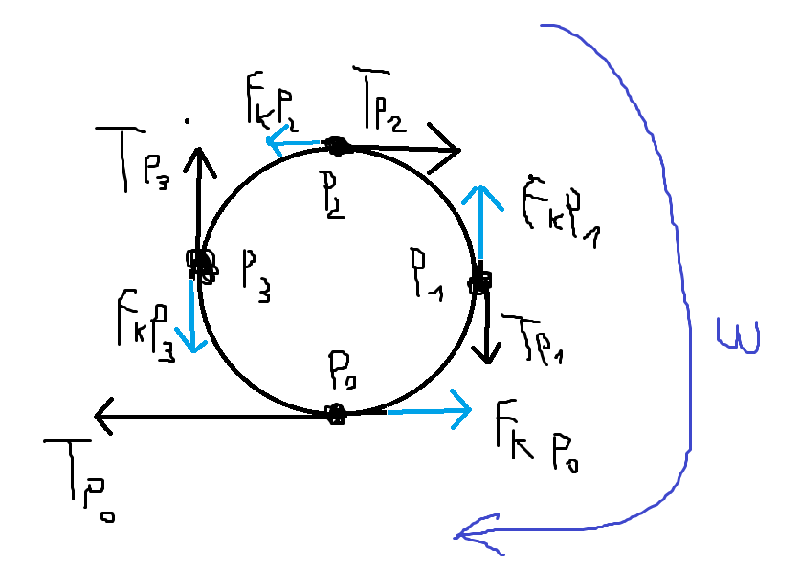 Si el cilindro gira en la direccion de w, es porque la correa le esta ejerciendo la tension en esa "direccion", despues es cierto que aparece una fuerza de friccion (que supongo que es dinamica porque no se dice que sea ideal la correa) en cada punto en direccion contraria a donde lo quiere "llevar" la tension, por lo tanto los torques serian distintos y de direcciones opuestas
Si el cilindro gira en la direccion de w, es porque la correa le esta ejerciendo la tension en esa "direccion", despues es cierto que aparece una fuerza de friccion (que supongo que es dinamica porque no se dice que sea ideal la correa) en cada punto en direccion contraria a donde lo quiere "llevar" la tension, por lo tanto los torques serian distintos y de direcciones opuestas