buenas, estaba viendo un teórico y me surgió una duda, cuando hacen la derivada de una función y expresando en sus funciones generalizadoras, cuando tenes un producto de funciones, me estoy mareando un poco, porque lo hice de una forma que me parecio la mas robusta y no me da igual y no se que me esta faltando, despues lo hice de otra forma y llego, pero queria preguntar para aclarar un pooco
la otra forma es considerar como la funcion completa y no haciendo regla de la cadena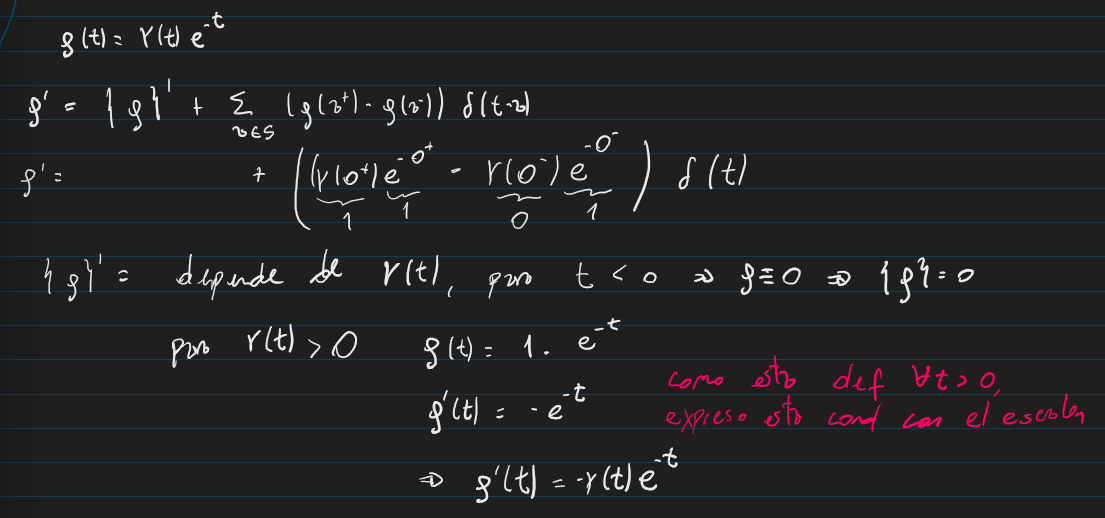
queria saber en que le estoy errando o que consideraciones no estoy tomando para hacerlo de la primer forma
Hola Nicolás,
cuando considerás "la función completa" (tu segunda hoja), parece que estás procediendo bien a "derivar la función donde es derivable y luego agregar deltas en los puntos de discontinuidad, con la amplitud del salto". Pero luego, al llevar esto adelante, hacés alguna cosa rara.
La función Y(t)e^{-t} es derivable en todo punto, salvo en el origen. En los t negativos, la función es idénticamente nula, por lo que tabién lo es su derivada. En los instantes positivos, la derivada vale -e^{-t}. Entonces, "la derivada como función donde es derivable", vale -Y(t).e^{-t}. Ahora hay que sumar una delta en el punto de discontinuidad t=0. La amplitud de la delta la da el salto (con signo), que en este caso vale 1 (límite por la derecha menos límite por la izquierda).
Entonces ( Y(t).e^{-t} )' = delta(t) - Y(t).e^{-t}
Fijate bien si te queda claro, e intentá luego hacer la derivada de la función h(t) de las diapos.
Saludos,
Pablo
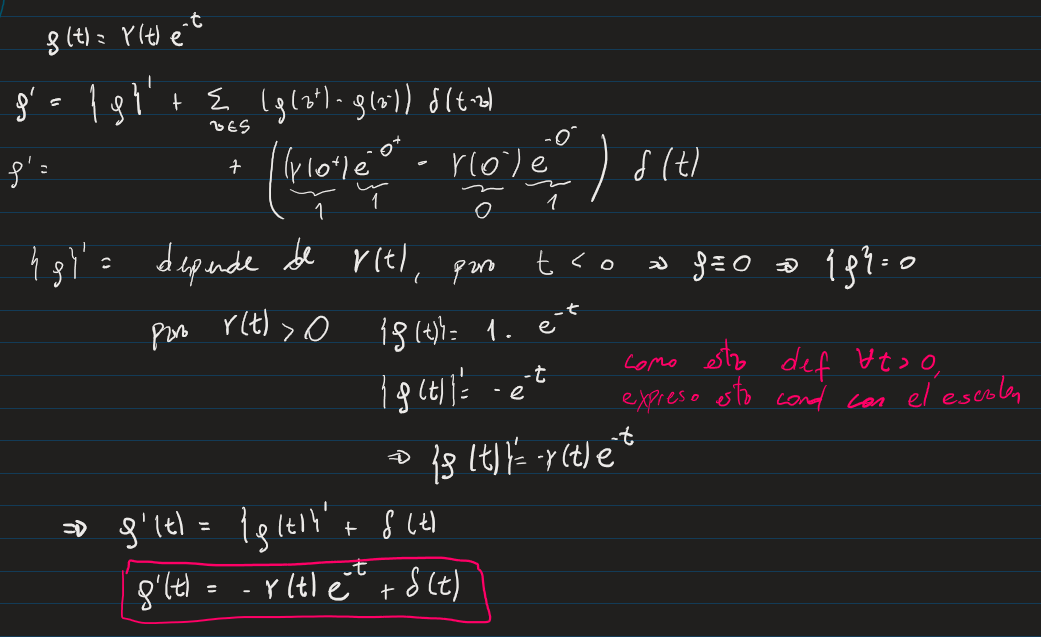
(ahi lo corregi)
mi pregunta es mas sobre la primera forma, que es lo que falla al derivar la funcion cuando aplico la regla de la cadena para y deerivo cada funcion como si derivase una funcion generalizadora
no sé si te estás refiriendo a derivar el prodcto ( Y(t).e^{-t} )' con la regla del producto. Ahí también funciona:
( Y(t).e^{-t} )' ) = Y'(t).e^{-t} + Y(t).( e^{-t} ) ' = e^{-t} . delta(t) - Y(t).e^{-t} = delta(t) - Y(t).e^{-t}
donde hay que usar que la "propiedad de muestreo" alfa(t).delta(t) = alfa(0).delta(t)
Saludos,
Pablo