Hola,
Una consulta, en la letra del Ejercicio 3 del Práctico 3, en la Sugerencia se dice que la condición para la reconstrucción perfecta con OLA implica la siguiente igualdad:
![y[n] = x[n]\left( \sum_{r=-\infty}^{+\infty} w_{Hann}[rR-n] \right) = x[n] y[n] = x[n]\left( \sum_{r=-\infty}^{+\infty} w_{Hann}[rR-n] \right) = x[n]](https://eva.fing.edu.uy/filter/tex/pix.php/02280428f091e50dd41c9c1761807997.gif)
Lo que a mi entender implica que:
![\sum_{r=-\infty}^{+\infty} w_{Hann}[rR-n] = 1 \sum_{r=-\infty}^{+\infty} w_{Hann}[rR-n] = 1](https://eva.fing.edu.uy/filter/tex/pix.php/c95a88bd39b173c2799fc0525511c635.gif)
Mientras que en la diapositiva 7 de las clases 12, 13 y 14 se dice que para la reconstrucción perfecta con OLA implica la siguiente igualdad:
![\sum_{r=-\infty}^{+\infty} w_{Hann}[rR-n] = \frac{W_{Hann}(e^{j0})}{R} \sum_{r=-\infty}^{+\infty} w_{Hann}[rR-n] = \frac{W_{Hann}(e^{j0})}{R}](https://eva.fing.edu.uy/filter/tex/pix.php/55cf42d697d0895e45051baff6ea2460.gif)
Mi duda es, a que resultado debería llegar en esta parte de este ejercicio del el práctico (para los casos
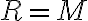 o
o 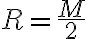 , siendo
, siendo 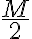 entero)?
entero)?Agrego captura de la diapositiva en cuestión:
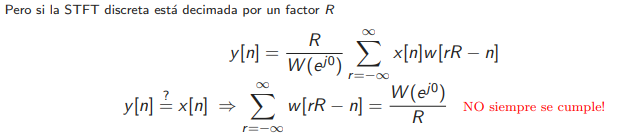
Muchas gracias!
Saludos,
Francisco