Gracias Matteo! Me sentí motivado a demostrarlo, y , mientras lo intenté, descubrí que mi algoritmo tenía una falla. De todas formas, se me ocurrió cómo arreglar esa falla, y sigue siendo un algoritmo más sencillo y menos entreverado que el visto en e curso.
Voy a anexar mi intento de demostración, y voy a explicar en qué momento me di cuenta que fallaba. Mi demostración comenzó así:
"Creo que es más sencillo demostrar la equivalencia entre ambos algoritmos que demostrar desde cero que mi versión es correcta. Se me ocurre lo siguiente:
Idea de la demostración: Las versión presentada en el curso y la versión simplificada no son tan diferentes. La idea es mostrar que cada diferencia no cambia el resultado del algoritmo.
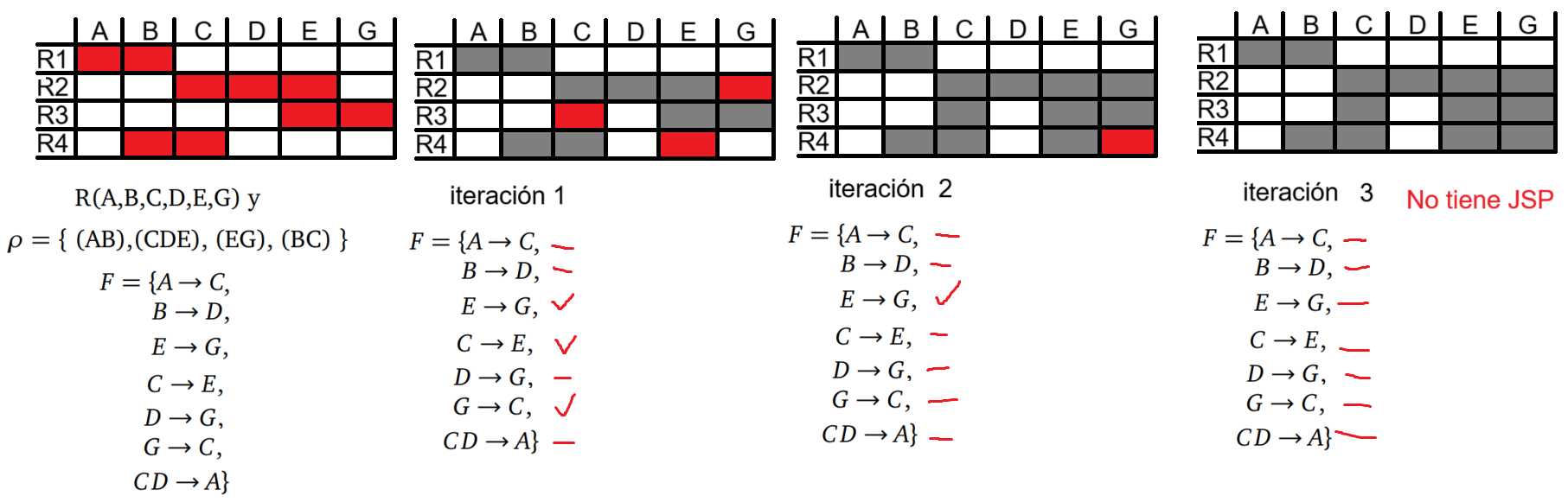
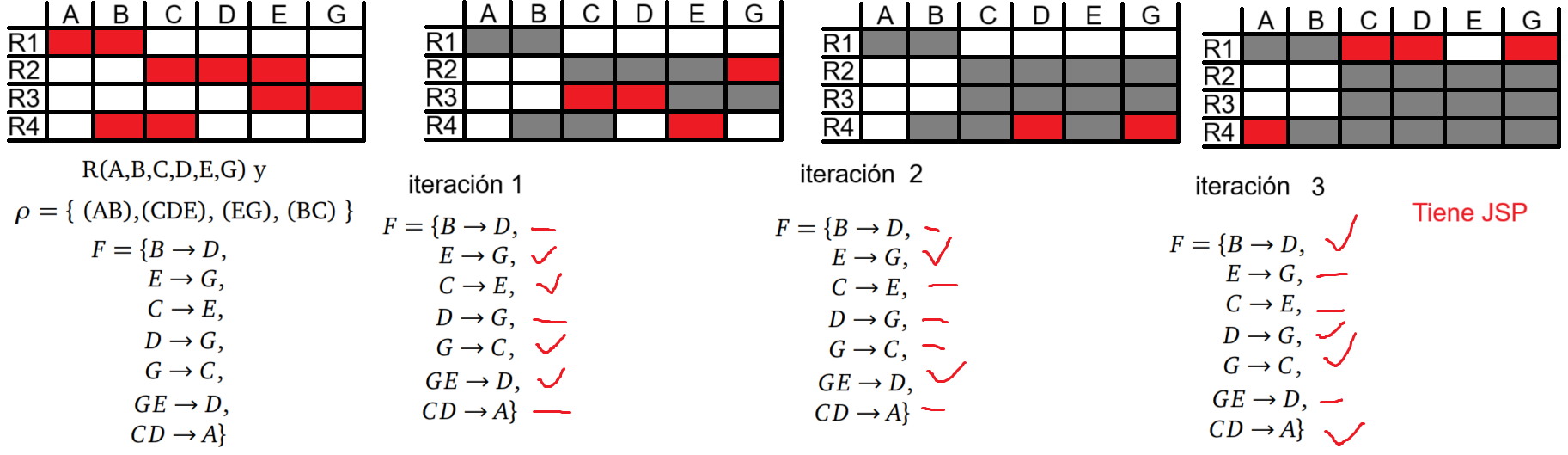
Hipótesis: El algoritmo propuesto en el curso es correcto, es decir, termina, y devuelve el resultado correcto (cuando la descomposición tiene JSP, siempre se llega a una fila completa de "a"s, y cuando no la tiene, el algoritmo termina antes de llegar a una fila completa de "a"s).
Tesis: La versión simplificada del algoritmo es correcta.
Demostración:
La versión mostrada en el curso del algoritmo es correcta, por hipótesis. Dicha versión difiere de la versión simplificada únicamente en los subíndices de las entradas de la matriz. Hay dos diferencias:
(i) Se sustituyen las "ai" del algoritmo del curso por un booleano (donde i es la columna de la entrada de la matriz).
(ii) Se sustituyen las "bi,j" del algoritmo del curso por un booleano (donde i y j son la columna y fila de la entrada de la matriz, respectivamente)
(iii) Se sustituyen los valores iniciales (previos a la primera iteración) de "ai" y "bi,j" por "true" y "false" respectivamente.
Veamos que antes y después de aplicas estas sustituciones, el algoritmo es equivalente.
Equivalencia de (i):
Como la asignación de ai en el algoritmo se realiza para las mismas columnas en cada fila, la indicación de la columna es innecesaria. Es decir, para cada ai, el valor de i es siempre el mismo valor al de la columna en la que se encuentra, y ninguna asignación en el algoritmo asigna un valor de ai de una columna, a otra columna distinta, por lo que el valor de i se puede inferir totalmente de la columna en la que se encuentra (su explicitación como subíndice es innecesaria).
Equivalencia de (ii):
Cada bi,j cuenta con un índice que indica su columna, y otro que indica su fila. Para el caso de las columnas, el razonamiento es análogo que en "Equivalencia de (i)". Para el caso de las filas ..."
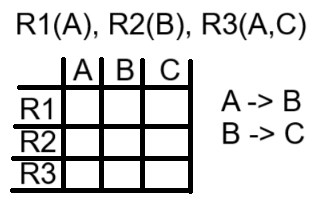
Acá es cuando me di cuenta que mi versión del algoritmo no estaba contemplando algo. En el algoritmo original sí hay asignaciones entre filas distintas, por lo que el número de filas sí era un valor relevante de la notación (a diferencia del de columnas). Esto implica que las dependencias transitivas no están siendo tenidas en cuenta cuando alguno de los atributos no pertenece a ninguno de los esquemas. Para ilustrar con un ejemplo:
si tenemos esa descomposición, con los siguientes estados iniciales para ambas versiones del algoritmo:
Al considerar la primera dependencia funcional, la versión simplificada del algoritmo no hace nada, mientras que la original hace una asignación en la misma fila entre dos valores "b"
Esto es un error en mi versión del algoritmo, ya que al considerar la siguiente dependencia, los resultados son distintos porque en la versión simplificada no se tuvo en cuenta la transitividad entre atributos que no están en las tablas involucradas.
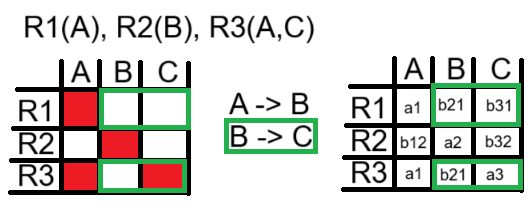
Si bien parece que todo está bien, porque los valores de verdadero y falso coinciden, solo lo hacen porque se aplicó primero A -> B. Si no existiera esa dependencia, mi algoritmo marcaría (R1,C), mientras que el algoritmo original no.
Por suerte, haber encontrado ese error mientras intentaba hacer la demostración me hizo darme cuenta que el valor de las filas sí es importante, por lo que este problema se resolvería simplemente añadiendo los valores de las filas a cada entrada:
En este caso, la primera iteración sí sería idéntica:
Y se resolvería el problema de las transitividades en los atributos que no forman parte de las tablas. Entonces, habiendo hecho este cambio en el algoritmo, la demostración sería distinta en el punto 2, que generaba problemas:
Demostración:
La versión mostrada en el curso del algoritmo es correcta, por hipótesis. Dicha versión difiere de la versión simplificada únicamente en los subíndices de las entradas de la matriz. Hay dos diferencias:
(i) Se sustituyen las "ai" del algoritmo del curso por un booleano (donde i es la columna de la entrada de la matriz).
(ii) Se sustituyen las "bi,j" del algoritmo del curso por un booleano (donde i y j son la columna y fila de la entrada de la matriz, respectivamente)
(ii) Se sustituyen las "bi,j" del algoritmo del curso por un entero j (donde i y j son la columna y fila de la entrada de la matriz, respectivamente)
(iii) Se sustituyen los valores iniciales (previos a la primera iteración) de "ai" y "bi,j" por "true" y "false" respectivamente.
(iii) Se sustituyen los valores iniciales de (previos a la primera iteración) de "ai" y "bi,j" por "true" y el número de columna de la entrada respectivamente.
Veamos que antes y después de aplicas estas sustituciones, el algoritmo es equivalente.
Equivalencia de (i):
Como la asignación de ai en el algoritmo se realiza para las mismas columnas en cada fila, la indicación de la columna es innecesaria. Es decir, para cada ai, el valor de i es siempre el mismo valor al de la columna en la que se encuentra, y ninguna asignación en el algoritmo asigna un valor de ai de una columna, a otra columna distinta, por lo que el valor de i se puede inferir totalmente de la columna en la que se encuentra (su explicitación como subíndice es innecesaria).
Equivalencia de (ii):
Cada bi,j cuenta con un índice que indica su columna, y otro que indica su fila. Para el caso de las columnas, el razonamiento es análogo que en "Equivalencia de (i)". y las filas están contempladas en el entero j, ya que las asignaciones entre números de fila son sustituídas por asignaciones entre enteros que representan esos números de fila
Equivalencia de (iii):
Como los valores iniciales de las entradas de la matriz son ai y bi,j en la versión del algoritmo vista en el curso, y los valores iniciales de las entradas de la matriz son "true" y "i" en la versión simplificada, y las equivalencias de (i) y (ii) están demostradas arriba, el estado inicial de la matriz no pierde información con respecto al estado inicial de la matriz en la versión original del algoritmo."
En resumen, lo único en lo que consiste la simplificación es en eliminar los números de columna de todas las entradas, ya que no ocurre ninguna sustitución entre elementos de distintas columnas en la ejecución del algoritmo.
Muchas gracias Matteo por animarme a realizar esta demostración.