Foro general

Al final de la clase de hoy nos quedamos discutiendo un ejercicio del Práctico 7: Ejercicios de evaluaciones anteriores // 1) Segundo parcial del segundo semestre 2023 // El límite de la función en el origen no existe por lo siguiente: El candidato a límite es 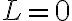$L=0$, pero si se escribe la función usando coordenadas polares, fuera de la región 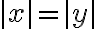$|x|=|y|$, queda 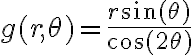$g(r,\theta)=\frac{r \sin(\theta)}{\cos(2\theta)}$. 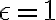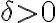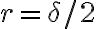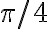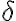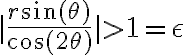Y para $\epsilon =1$, por ejemplo, para cualquier $\delta >0$ se puede tomar $r=\delta/2$ y $\theta$ arbitrariamente cerca de $\pi/4$, de manera que ese punto está en la bola de radio $\delta$ pero cumple $|\frac{r \sin(\theta)}{\cos(2\theta)}|> 1 = \epsilon$.