T= ICMα tiene que ser planteado tanto para la polea como para el disco o como sería
Gracias
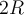 como para la polea de radio
como para la polea de radio 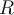 . Tené en cuenta que aunque los dos sean discos, el momento de inercia es distinto porque sus radios son distintos.
. Tené en cuenta que aunque los dos sean discos, el momento de inercia es distinto porque sus radios son distintos. Saludos
Piero
(Editado por Nicolás Casaballe - envío original sábado, 26 de octubre de 2024, 18:12)

Hola, Santiago. Tu planteo está muy bien encaminado. Me parece perfecto que al llegar a un resultado que no concuerda con las expectativas (T2 = 0 ) adviertas que algo no está funcionando (desearía que todos los estudiantes procedieran de esta manera).
Hay un error de signo algo sutil que es difícil de advertir en este tipo de ejercicios. Voy a intentar explicar cómo ocurre. Sustancialmente el problema se origina al definir implícitamente el sentido positivo del eje perpendicular al dibujo. Fijate que en tu hoja están señalados los vectores unitarios i, j, pero falta indicar k.
Al escribir la ecuación de vínculo al comienzo,  , estás estableciendoo que las variables que representan las componentes de la aceleración
, estás estableciendoo que las variables que representan las componentes de la aceleración 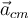 y la aceleración angular
y la aceleración angular  en sus respectivos ejes van a tener el mismo signo. O bien son ambas positivas, o bien son ambas negativas.
en sus respectivos ejes van a tener el mismo signo. O bien son ambas positivas, o bien son ambas negativas.
Cuando el centro del disco acelera en el mismo sentido que el vector i, como rueda sin deslizar, su aceleración angular es un vector entrante al dibujo. En este caso  y, por lo tanto, para aplicar la ecuación de vínculo anterior, el vector k debe ser elegido entrante al dibujo también. De esa forma obtenemos
y, por lo tanto, para aplicar la ecuación de vínculo anterior, el vector k debe ser elegido entrante al dibujo también. De esa forma obtenemos  (podríamos pretender elegir el sentido contrario para k, pero deberíamos modificar la ecuación de vínculo entonces).
(podríamos pretender elegir el sentido contrario para k, pero deberíamos modificar la ecuación de vínculo entonces).
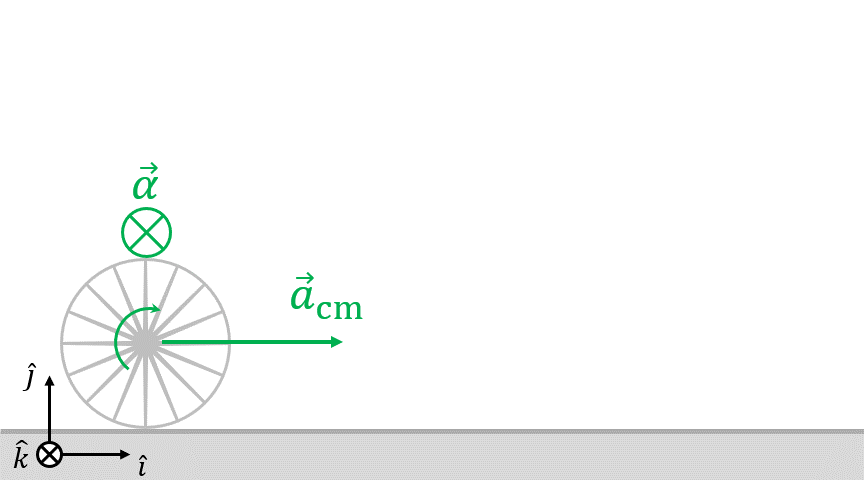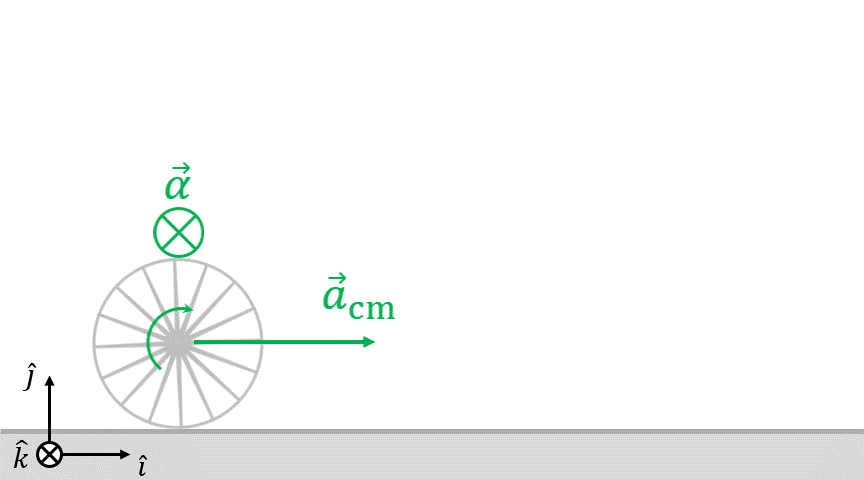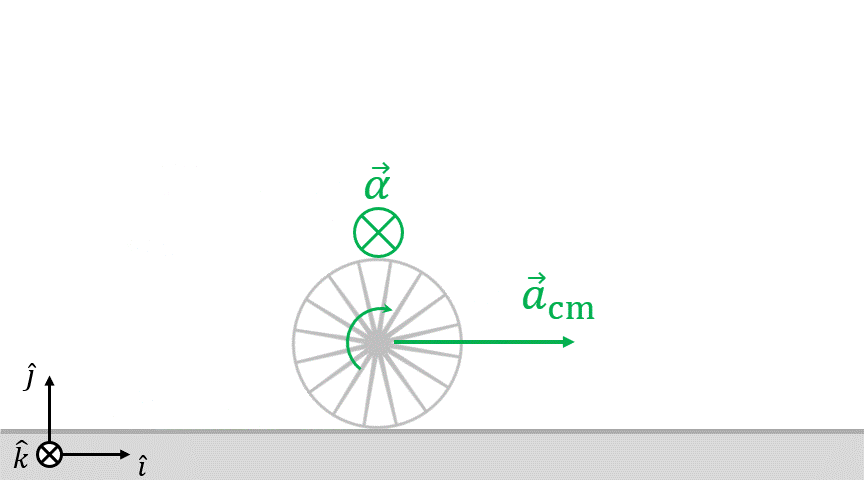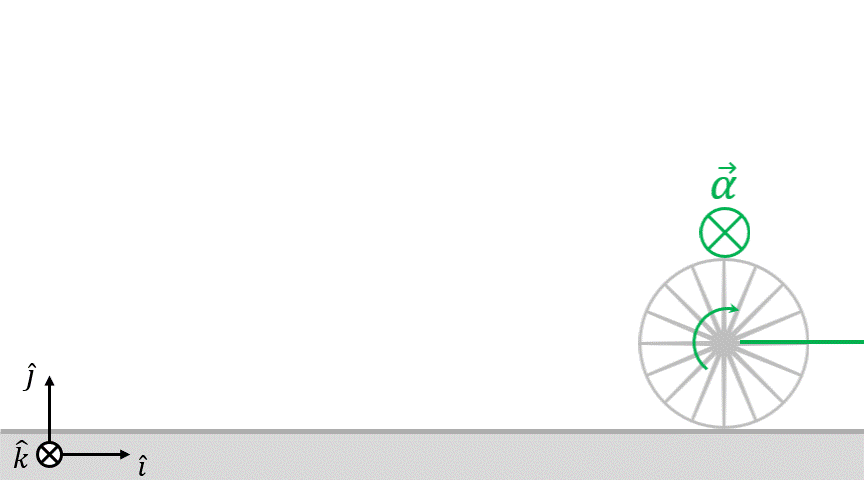
Más adelante, en la ecuación para el torque neto, hay que tomar en cuenta el sentido del vector k. Según el planteo que realizaste y la forma en que está dibujada la fuerza de rozamiento 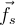 , el torque que realiza con respecto al centro del disco es entrante al dibujo. Entonces, este torque
, el torque que realiza con respecto al centro del disco es entrante al dibujo. Entonces, este torque  apunta en el mismo sentido que el vector k y su componente a lo largo de esta dirección es positiva.
apunta en el mismo sentido que el vector k y su componente a lo largo de esta dirección es positiva.
Colorín colorado: en tu ecuación (III) tienes que cambiar el signo del torque de la fuerza de rozamiento. A partir de ahí, haciendo prácticamente las mismas operaciones que ya planteaste, deberías poder llegar al resultado del ejercicio.
Mucha suerte!
NC