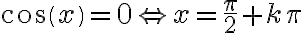Ejercicio diciembre 2021

Ejercicio diciembre 2021

de Mateo Roman Allonca Maldonado -
Número de respuestas: 4

Hola, me gustaría analizar este ejercicio: 


Lo primero que hice fue analizar el conjunto B, que son los puntos aislados que cumplen que cos(x)= 0 y sen(x)= -1. Por ejemplo, para la función cos(x) 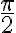 \frac{ \pi }{2} , mientras que para sen(x)  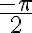\frac{- \pi }{2} . Me gustaría saber si mi razonamiento es correcto, caso contrario por favor corregirme.
para i), es verdadero. Ya que al ser puntos aislados, si me tomo una bola de entorno cualquiera va a tener puntos que no pertenecen a B.

para ii), si B es cerrado, entonces su complemento es abierto. El complemento de B es R^2 menos los puntos de B, que como dijimos anteriormente son aislados. Si su complemento es abierto, entonces no incluye la frontera. Entonces B si incluye a la frontera. Pero como B son puntos aislados, es un absurdo ya que no tiene puntos frontera. 

parte iii) un punto es de acumulación de un conjunto si tomamos una n-bola(x) que contiene por lo menos un punto del conjunto sin ser x (su centro). Leí en una parte en el libro de Apostol que aquellos puntos que no son de acumulación, entonces son aislados. ¿Vale el recíproco? 


Me queda la duda de como formular la parte III) para resolver el ejercicio. Un saludo. 
En respuesta a Mateo Roman Allonca Maldonado

Re: Ejercicio diciembre 2021

de Rafael Parra -
Hola Mateo, tu razonamiento con respecto a los puntos es correcto. Te recomiendo solamente que los expreses de forma general, por ejemplo,  cos(x)=0 \Leftrightarrow x=\dfrac{\pi}{2}+k\pi variando el parámetro sobre todos los enteros. De igual forma para los valores de la y. En este caso, todas las afirmaciones son verdaderas. Para el caso 3, es verdad lo que afirmas, en este caso el complemento de B es abierto y todos los puntos de B son de acumulación para B^c.

Saludos 
En respuesta a Rafael Parra

Re: Ejercicio diciembre 2021

de Mateo Roman Allonca Maldonado -
Hola Rafael, tengo una duda sobre la III). Como los puntos de B son aislados, entonces si me tomo un n-bola de radio r va a tener puntos que no sean de B y si de B complemento. Por lo tanto si lo miramos desde B complemento, esos puntos son de acumulación, ya que las n-bolas de los puntos (sin tomar en cuenta el centro) tendrán puntos del mismo B complemento. ¿Es correcta la afirmación?

Por otro lado, yo había deducido que la 2 es falsa. No entiendo por qué es verdadera, ¿Podrías explicarme? Gracias y saludos.
En respuesta a Mateo Roman Allonca Maldonado

Re: Ejercicio diciembre 2021

de Rafael Parra -
Hola Mateo. En relación con la Parte II, cuando mencionas puntos aislados, es importante que especifiques con respecto a qué conjunto te estás refiriendo. Al hacer la afirmación "El complemento de B es \mathbb{R}^2 menos los puntos de B, que como dijimos anteriormente son aislados", debes aclarar que se trata de puntos aislados de B.

Para mostrar que B es cerrado, puedes hacerlo directamente de la definición. Es decir, mostrar que B^c es abierto. Consideras cuanquier puento (x_0,y_0)\in B^c y es muy sencillo construir una Bola centrada en este punto totalmente contenida en B^c.
Con respecto a lo que dices de la afirmación III es correcto, todos los puntos de $B$ son de acumulación para B^c.

Saludos