Hola Juan.
En el libro se trata un tipo de problemas de tipo dividir y conquistar en los que las subinstancias tienen el mismo tamaño, que es la mitad del tamaño de la instancia de entrada, y que en la relación de recurrencia el tiempo de dividir la instancia y luego combinar los resultados se representa con
donde 
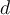es un entero no negativo.
En particular, el exponente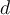 puede ser 0. Y lo que decís, "ya que todo lo que se hace adentro de cada invocación recursiva es O(1)", implica no que 
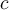sea 1, sino que 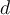es 0.
En el libro se trata un tipo de problemas de tipo dividir y conquistar en los que las subinstancias tienen el mismo tamaño, que es la mitad del tamaño de la instancia de entrada, y que en la relación de recurrencia el tiempo de dividir la instancia y luego combinar los resultados se representa con
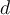donde es un entero no negativo. En particular, el exponente
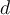puede ser 0. Y lo que decís, "ya que todo lo que se hace adentro de cada invocación recursiva es O(1)", implica no que 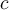sea 1, sino que 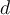es 0.El tiempo de ejecución es cierto que es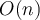 
, pero esta no es una cota ajustada, no es 
. De manera no rigurosa, si fuera , y el procesamiento en cada nodo es 
entonces el algoritmo visitaría todos los nodos una vez. Y tu algoritmo no hace eso, sino que aprovecha que el árbol es de búsqueda (está ordenado) y solo recorre un camino desde la raíz hasta posiblemente una hoja, que, como el árbol está balanceado tiene profundidad 
.
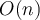, pero esta no es una cota ajustada, no es . De manera no rigurosa, si fuera , y el procesamiento en cada nodo es entonces el algoritmo visitaría todos los nodos una vez. Y tu algoritmo no hace eso, sino que aprovecha que el árbol es de búsqueda (está ordenado) y solo recorre un camino desde la raíz hasta posiblemente una hoja, que, como el árbol está balanceado tiene profundidad . Saludos.