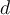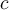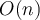Prog3: Practico calentamiento 7

Buenas,
la parte 1 queda asi

Como estamos en divide y vencerás el tiempo de ejecución es de la forma T(n)<=qT(n/2) +cn

después (creo) estamos en el caso de q=1 del libro de la propiedad (5.3) ya que el algoritmo tiene una dicotomia para volver a invocar o la rama izquierda o la derecha entonces se cumple que,
para alguna constante c : T(n) <= T(n/2) + cn.
¿Puedo decir que c=1 ya que todo lo que se hace adentro de cada invocación recursiva es O(1)?
¿Es valido dibujar un árbol para decir que el patrón para una instancia de un nivel de recursión j arbitraria es de tamaño cn/2^j?
¿Para hallar el ultimo valor de j de la sumatoria que resuelve la parte derecha de la recurrencia, siempre tengo que igualar el tamaño de la instancia de nivel arbitraria j-esima a 1? ¿o depende del caso base?
Luego el libro hace lo siguiente: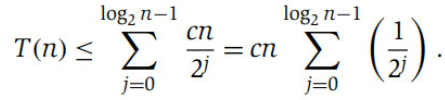

y queda por ser suma geométrica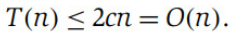

entonces no se que estoy haciendo mal porque el ejercicio pide que sea O(log n) el tiempo de ejecución.

Re: Practico calentamiento 7

de Fernando Fernandez - viernes, 11 de octubre de 2024, 08:59

Hola Juan.
En el libro se trata un tipo de problemas de tipo dividir y conquistar en los que las subinstancias tienen el mismo tamaño, que es la mitad del tamaño de la instancia de entrada, y que en la relación de recurrencia el tiempo de dividir la instancia y luego combinar los resultados se representa con

$c \cdot n^d$ donde

En particular, el exponente

$d$ puede ser 0. Y lo que decís, "ya que todo lo que se hace adentro de cada invocación recursiva es O(1)", implica no que

$c$ sea 1, sino que

$d$ es 0.

El tiempo de ejecución es cierto que es

$O(n)$ , pero esta no es una cota ajustada, no es

$\Theta(n)$ . De manera no rigurosa, si fuera

$\Theta(n)$ , y el procesamiento en cada nodo es

$\Theta(1)$ entonces el algoritmo visitaría todos los nodos una vez. Y tu algoritmo no hace eso, sino que aprovecha que el árbol es de búsqueda (está ordenado) y solo recorre un camino desde la raíz hasta posiblemente una hoja, que, como el árbol está balanceado tiene profundidad

$\Theta(\log n)$ .

Saludos.