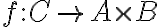tal que f(c)=(a,b) donde a es el resto de dividir entre m y b lo mismo pero entre n. Quería consultar que para probar biyectividad parte de la base de que 
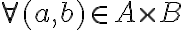se cumple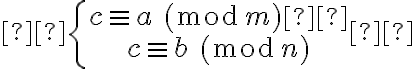
No entiendo bien cómo puede asumir eso.
Buenas! Quería preguntar sobre la demo de esto, que toma una función biyectiva tal que f(c)=(a,b) donde a es el resto de dividir entre m y b lo mismo pero entre n. Quería consultar que para probar biyectividad parte de la base de que se cumple
No entiendo bien cómo puede asumir eso.
tal que f(c)=(a,b) donde a es el resto de dividir entre m y b lo mismo pero entre n. Quería consultar que para probar biyectividad parte de la base de que se cumpleNo entiendo bien cómo puede asumir eso.
En respuesta a Juan Agustín Rivero Szwaicer
Re: $$\varphi(mn)=\varphi(m)\varphi(n)$$
de Gabriel Mello -
Hola.
Que ese sistema tenga solución y sea única entre 0 y mn-1 es exactamente el enunciado del teorema chino del resto. Aparte de eso hay que probar que como a es coprimo con n y b es coprimo con m entonces c es coprimo con mn.
Saludos,
Gabriel