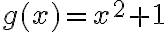Buen día Lucía.
En realidad siempre que hacemos uso de equivalencias de dos funciones, estamos usando Taylor de manera indirecta.
Ej1: Cuando decimos que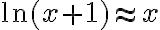 (es decir son equivalentes/o se aproximan/ cuando
(es decir son equivalentes/o se aproximan/ cuando  )
)
Ej2: O cuando se dice que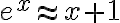 (cuando
(cuando  ).
).
Ambas son resultados de Taylor.
Solo que habrá casos en las que tenemos que encontrar funciones mucho mas próximas, las cuales seguirán siendo resultado de Taylor.
Ej1: Una función que más se aproxima a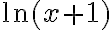 es
es 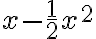 (cuando
(cuando  )
)
Te voy ayudar con el ejercicio 9.
Otra forma de encontrar de manera mas rápido un polinomio de Taylor, y evitarte esas cuentas tediosas.
1°) Tenemos que observar que lo podemos mirar como una composición de funciones.
lo podemos mirar como una composición de funciones.
En realidad siempre que hacemos uso de equivalencias de dos funciones, estamos usando Taylor de manera indirecta.
Ej1: Cuando decimos que
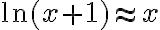 (es decir son equivalentes/o se aproximan/ cuando
(es decir son equivalentes/o se aproximan/ cuando  )
)Ej2: O cuando se dice que
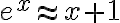 (cuando
(cuando  ).
).Ambas son resultados de Taylor.
Solo que habrá casos en las que tenemos que encontrar funciones mucho mas próximas, las cuales seguirán siendo resultado de Taylor.
Ej1: Una función que más se aproxima a
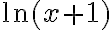 es
es 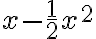 (cuando
(cuando  )
)Te voy ayudar con el ejercicio 9.
Otra forma de encontrar de manera mas rápido un polinomio de Taylor, y evitarte esas cuentas tediosas.
1°) Tenemos que observar que
 lo podemos mirar como una composición de funciones.
lo podemos mirar como una composición de funciones. entonces 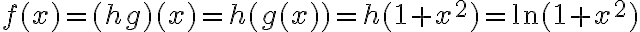 .
.
2°) Ya por cálculo 1, sabemos que el polinomio de Taylor por definición de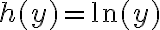 cerca de
cerca de  es:
es:
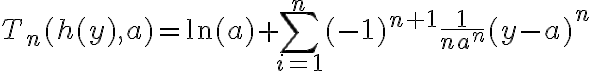 .
.
3°) Observar que cuando la función
la función  .
.
4°) Calculamos Taylor de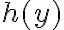 con
con 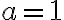 .
.
 .
.
5°) Basta reemplazar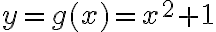 .
.
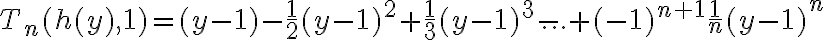 .
.
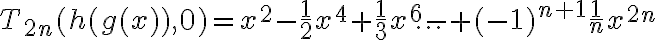 .
.
6°) Podemos aproximar la función convenientemente:
convenientemente:
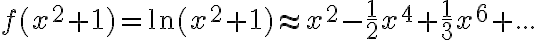
Observación1: Basta considerar los dos primeros términos de la aproximación anterior (Si consideras más términos el resultado es el mismo, solo que un poquito más exacto).
Observación2: Esta propiedad funciona bien para cualquier polinomio . (Se podría extender a otras funciones, pero es ir teniendo cuidados con los dominios).
. (Se podría extender a otras funciones, pero es ir teniendo cuidados con los dominios).
Espero que mi sugerencia te ayude, con ejercicios similares al .
.
Si algo mas quieres detallar o que se aclare estaré pendiente.
Saludos.
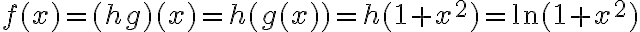 .
. 2°) Ya por cálculo 1, sabemos que el polinomio de Taylor por definición de
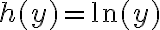 cerca de
cerca de  es:
es: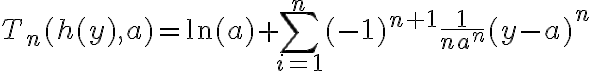 .
.3°) Observar que cuando
 la función
la función  .
.4°) Calculamos Taylor de
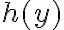 con
con 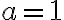 .
. .
.5°) Basta reemplazar
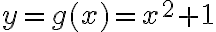 .
.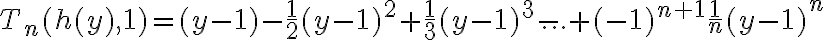 .
.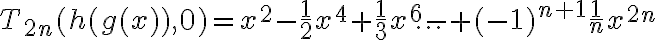 .
.6°) Podemos aproximar la función
 convenientemente:
convenientemente: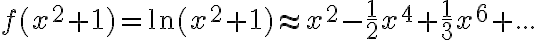
Observación1: Basta considerar los dos primeros términos de la aproximación anterior (Si consideras más términos el resultado es el mismo, solo que un poquito más exacto).
Observación2: Esta propiedad funciona bien para cualquier polinomio
 . (Se podría extender a otras funciones, pero es ir teniendo cuidados con los dominios).
. (Se podría extender a otras funciones, pero es ir teniendo cuidados con los dominios).Espero que mi sugerencia te ayude, con ejercicios similares al
 .
. Si algo mas quieres detallar o que se aclare estaré pendiente.
Saludos.