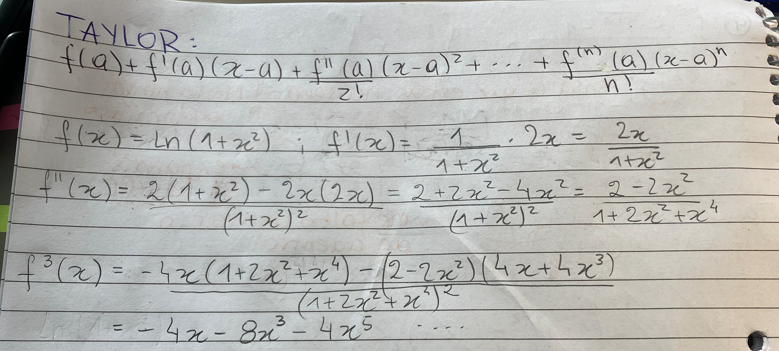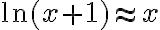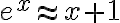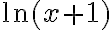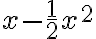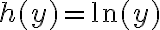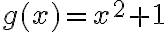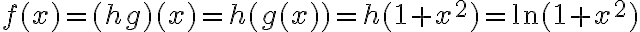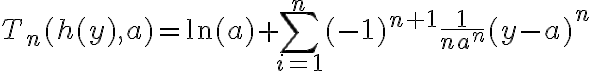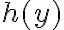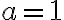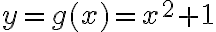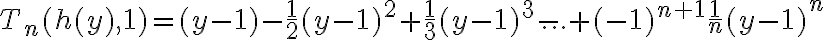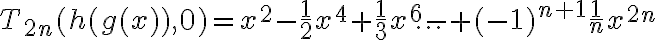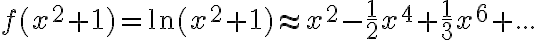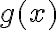El tema es que si yo no hacía taylor (lo que está en amarillo) como 1/x tiende a cero entonces e^(1/x) tiende a uno, no? Entonces te queda que diverge, o sea lo opuesto a lo que tendría que dar. Hay algo mal en ese razonamiento?
Así que no entiendo bien cuándo usar Taylor.
A su vez, para el ej 9 de parcial 2do semestre 2021, hay que usar el Taylor cuarto, y queda suuper tedioso hacerlo, no hay alguna forma de simplificarlo? Es la última foto
Graciass