Foro de consultas generales

Hola, dejo acá una guía de cómo pensar esta parte del ejercicio, a pedido de un estudiante (Santiago) que se quedó conversando conmigo al final de la clase del miércoles.

Itinerario:

1) Demostrar que las soluciones a ecuaciones diferenciales autónomas son inyectivas (suponer que no y aplicar Teoremas de Rolle y Picard para obtener una contradicción)

2) Concluir que las soluciones de la ecuación tienen derivada inyectiva.

3) Suponer que $\forall T>0, \exists t_0>T: \varphi(t_0) \geq \sqrt{t_0}$ y probar que en estas condiciones existe y es único 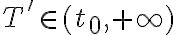$T' \in (t_0,+\infty)$ tal que $\varphi(T')=\sqrt{T'}$.

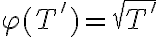4) Probar que 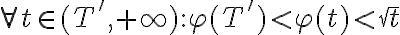$\forall t \in (T',+\infty): \varphi(T') < \varphi(t) < \sqrt{t}$ y por lo tanto 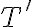$T'$ contradice el supuesto.

Les aconsejo hacer dibujitos para entender bien lo que está pasando. Cualquier cosa, pregunten. ¡Saludos!