Buenas! Espero se encuentren bien.
El ejercicio es el siguiente
La solución que se nos ocurrió con unos compañeros fue la siguiente (debería decir Endwhile)
Nuestras dudas son :
1) Esta idea y solución, es correcta?
2) Para demostrar la corrección no utilizamos ni Stay ahead ni Exchange argument. Nuestra solución va mas por el lado de las etiquetas, encontramos n casas distintas que si o si necesitan etiquetas distintas. Pero en realidad es un caso distinto, ya que en el ejemplo de las etiquetas ya teníamos los intervalos al principio, cuando aquí los vamos creando nosotros y no sabemos cuantos tenemos al principio para calcular el depth. Está mal no basarse directamente en ninguna de las 3 opciones?
3) En el paso número 7, no hace falta especificar más? En el libro lo escriben de esta manera "vaga", pero dependiendo de que forma lo hagas cambia el tiempo de ejecución, podría llegar a tener tiempo de ejecución total O(n^2) cuando hay opciones mas rápidas.
Muchas gracias!
Saludos,
Diego Furrer.
Hola Diego.
Está bien, en una muy buena solución.
1) Acá supongo que te referís al algoritmo. Tal vez en el paso 4 podría decirse Sea c la primera casa de C. En el paso 5 'agregamos' no parece adecuado. Podría ser mejor unir los pasos 5 y 6.
2) La técnica de encontrar una cota estructutal es válida y es posible que ayude a entender mejor la esencia del problema. Sin embargo tiene el inconveniente de que puede ser más difícil aplicarla.
En este caso, lo que hicieron ustedes está muy bien.
Está bien, en una muy buena solución.
1) Acá supongo que te referís al algoritmo. Tal vez en el paso 4 podría decirse Sea c la primera casa de C. En el paso 5 'agregamos' no parece adecuado. Podría ser mejor unir los pasos 5 y 6.
2) La técnica de encontrar una cota estructutal es válida y es posible que ayude a entender mejor la esencia del problema. Sin embargo tiene el inconveniente de que puede ser más difícil aplicarla.
En este caso, lo que hicieron ustedes está muy bien.
La única observación que hago es en la primera frase.
- Empieza con el término intervalo, que todavía no fue definido (un intervalo sería un rango de largo 8 centrado en la coordenada donde se pone una estación).
- Se dice que la cantidad es n, pero ese símbolo ya fue usado para la cantidad de casas.
3) Depende de lo qué se pida. Si se pidera que el orden sea O(n) habría que dar un poco más de detalle. Pero parece bastante sencillo.
¿Cuál podría ser una solución 
.?
Saludos,
.? Saludos,
Buenas!
Muchas gracias por las observaciones, tienen todo el sentido.
En respuesta a la parte 3), es posible hacerlo en O(n)?
Nosotros habíamos pensado O(n) del paso 2 al 9, pero el paso 1 de ordenar las casas nos tomaría O(nlogn). Pensamos en ordenarlo al principio para que de esta forma el paso 7 de quitar las casas fuera sencillo, ya que las únicas casas que hay que revisar son las que vienen luego de la actual en la lista. Apenas encontramos una casa que esta más lejos que 8 de la casa "c" actual, podemos pasar a la siguiente iteración del while. Nosotros pensamos que si no las ordenáramos, siempre tendríamos que recorrer todas las casas, porque hasta la última en la lista podría ser quitada de C.
Y este último caso sería también el caso que generaría un tiempo de ejecución O(n^2). Aun teniendo las casas ordenadas, si no especificamos como las quitamos y no aprovechamos la ventaja que nos da que estén ordenadas, existe la opción de revisar todas las casas en cada iteración para saber cuales quitamos. En un set de casas donde todas estén a distancia mayor que 8, esto nos tomaría O(n^2).
Obviamente hay muchas maneras de evitar este caso, pero sin especificar la forma en la que quitamos las casas, daría espacio a una implementación O(n^2).
Ese fue nuestro razonamiento, aunque es verdad lo que decis, en este ejercicio no nos mencionan nada sobre el tiempo de ejecución, por lo que no hace falta especificar más.
Muchas gracias!
Saludos,
Diego Furrer.
Muchas gracias por las observaciones, tienen todo el sentido.
En respuesta a la parte 3), es posible hacerlo en O(n)?
Nosotros habíamos pensado O(n) del paso 2 al 9, pero el paso 1 de ordenar las casas nos tomaría O(nlogn). Pensamos en ordenarlo al principio para que de esta forma el paso 7 de quitar las casas fuera sencillo, ya que las únicas casas que hay que revisar son las que vienen luego de la actual en la lista. Apenas encontramos una casa que esta más lejos que 8 de la casa "c" actual, podemos pasar a la siguiente iteración del while. Nosotros pensamos que si no las ordenáramos, siempre tendríamos que recorrer todas las casas, porque hasta la última en la lista podría ser quitada de C.
Y este último caso sería también el caso que generaría un tiempo de ejecución O(n^2). Aun teniendo las casas ordenadas, si no especificamos como las quitamos y no aprovechamos la ventaja que nos da que estén ordenadas, existe la opción de revisar todas las casas en cada iteración para saber cuales quitamos. En un set de casas donde todas estén a distancia mayor que 8, esto nos tomaría O(n^2).
Obviamente hay muchas maneras de evitar este caso, pero sin especificar la forma en la que quitamos las casas, daría espacio a una implementación O(n^2).
Ese fue nuestro razonamiento, aunque es verdad lo que decis, en este ejercicio no nos mencionan nada sobre el tiempo de ejecución, por lo que no hace falta especificar más.
Muchas gracias!
Saludos,
Diego Furrer.
Perdón, fue un error mío, asumí que estabamos hablando de lo que corresponde a la línea 7. Todo el algoritmo es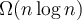 
por el paso 1.
Para la línea 7, y dado que C está ordenada y, como consecuencia, los que se deben remover son los primeros, cada remoción podría ser O(1). Por supuesto, como decís, podria no aprovecharse el ordenamiento obtenido en la línea 1 y llegar a
.
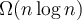por el paso 1.Para la línea 7, y dado que C está ordenada y, como consecuencia, los que se deben remover son los primeros, cada remoción podría ser O(1). Por supuesto, como decís, podria no aprovecharse el ordenamiento obtenido en la línea 1 y llegar a
.Perfecto, entonces si la letra pidiera que el orden fuera O(nlogn) sería necesario especificar mejor el paso 7?
Muchas gracias por las respuestas!
Saludos
Muchas gracias por las respuestas!
Saludos
Sí. Hay que explicar como, debido al ordenamiento del paso 1, cada remoción es O(1),
Excelente, muchas gracias!
Saludos
Saludos